二分图最大权完美匹配KM算法是在一个二分图里，求一个最大权匹配，但是要求这个匹配必须是完美匹配。如果匹配不一定是完美匹配，那么似乎只能将其转化为最小费用最大流来做了。我们可以使用KM算法对任意带权（无论正负权）二分图求最大/最小权完美匹配，它的算法复杂度是O(n³)，但是如果写得不好会变成O(n⁴)。

KM算法是通过给每个顶点一个标号（我们有时称之为顶标）来把求最大权匹配的问题转化为求完备匹配的问题的。我们令二分图中X部的节点的顶标为A_i，Y部的节点的顶标为B_i。X部与Y部节点之间的权值为W_i,j，那么，在算法进行的过程中，我们必须始终保持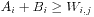成立。因为KM算法的正确性基于以下定理：

若由二分图中所有满足A_i+B_i=W_i,j的边 (i,j)构成的子图（称做相等子图）有完备匹配，那么这个完备匹配就是二分图的最大权匹配。

初始时为了使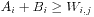成立，令A_i为所有与X_i顶点关联的边的权值的最大值，令B_i=0。如果当前的相等子图没有完备匹配，就需要修改顶标以使扩大相等子图，直到相等子图具有完备匹配为止（这样就可以求出最大权匹配）。

如果当前相等子图找不到完备匹配，那么是因为对于某个X顶点，我们找不到一条从它出发的交错路。这时我们获得了一棵交错树，现在我们把交错树中X部的顶点的顶标全都减小某个值d，Y部的顶点的顶标全都增加d，就可以使得至少有一条新边进入相等子图。这里d=min{A_i+B_i-W_i,j}，而且X_i在交错树中，Y_i不在。

但是如果仅仅是这样，用朴素的方法实现，算法复杂度是O(n⁴)。我们给每个Y部的顶点一个“松弛量”slack，每次开始找增广路时松弛量初始化为无穷大。在寻找增广路的过程中，检查边(i,j)时，如果它不在相等子图中，则让slack_j变成原值与A_i+B_i-W_i,j的较小值。这样，在修改顶标时，取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。但还要注意一点：修改顶标后，要把所有的slack_j值都减去d。经过这样一个优化实现后，算法复杂度就变成了O(n³)。 

• Relative Posts