题目在这里可以找到。
题目的大概意思是说,在整数格点的平面上有一个简单多边形(顶点坐标均为有理数),问其内部有多少格点。题目保证不会有格点出现在边界上。
三角剖分是不现实的,我们只能选择简单一些的梯形剖分。进而,我们需要计算一条直线下方的格点数目。这里的转化都比较简单,直接略过。接着,我们就把问题转化为了求一个这样的式子:
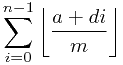
这是一个相当有趣的求值。显然,O(n)的算法并不能让我们满意。对于这个经典的问题,我们有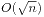 和
和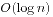 两种算法。
两种算法。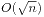 由于细节问题很多,我介绍的是
由于细节问题很多,我介绍的是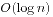 的算法。对
的算法。对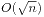 算法有兴趣的同学可以查看相关的论文。
算法有兴趣的同学可以查看相关的论文。
考察这个式子,首先,a和d都应该满足大于等于0,小于m的条件。否则我们可以通过变形得到新的a'和d'。我们如果要在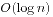 时间内计算出它的值,一定要设法缩小它的规模。我们将这个式子呈现在平面坐标系中,发现这其实就是求下面的一个图中
时间内计算出它的值,一定要设法缩小它的规模。我们将这个式子呈现在平面坐标系中,发现这其实就是求下面的一个图中
所有蓝色点的数目。所有的水平直线表示用来截取的y=km的常函数,红色的点则是(i,a+di)。问题到现在就是求每个点向下引射线,一共和这些直线能够有多少交点。显然,这些直线一共有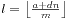 条。那么,我们对每条直线进行观察,发现如果我们只是求一条直线上有多少交点,是可以在O(1)的时间之内计算的。对于一条直线y=km,我们可以求出所有的交点数是
条。那么,我们对每条直线进行观察,发现如果我们只是求一条直线上有多少交点,是可以在O(1)的时间之内计算的。对于一条直线y=km,我们可以求出所有的交点数是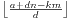 。
。
至此,问题的规模已经被缩小了,我们得到新的式子:
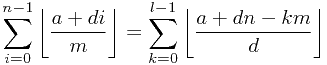
这里,我们需要对等式的右边进行一些细节处理,因为a+dn和m可能大于d。这样,我们成功的把问题规模缩小了,而这是一个类似取模的缩小方式,我们自然得到每次问题的规模至少被缩小到原来的一半,那么算法的复杂度就是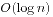 级别的。
级别的。