杭州赛区我们基本上没有犯什么严重的错误,但是反映了一个问题:代码速度太慢。个人觉得这次杭州的题目出的不错,不像Tianjin那样容易变得没有梯度,也不想Harbin那样只有2道难题。这次比赛一共有6道相对简单的题目,剩下的题目都是需要一定时间去做的。
比赛流程还是老样子,我全程都在读题,讲解题目意思。肖刘看完J之后觉得可以写,而我有没有发现什么一下子就可以写的题目,于是就让肖刘先写了。肖刘不负众望,1Y,这种递推、DP的题目肖刘还是很擅长的。然后我们讨论了一下所有题目的意思,觉得还是先写C和H,我轻松1Y了C,李晔晨也1Y了H。这时候已经有队伍4道题了。我们选择了跟一下题目,于是目前可以做的题目就是D、F。我们先写了F,WA了1次之后AC了。然后我们讨论了一下B,觉得是可以做的,于是就上去写,虽然中间犯了很多错误,但是还是AC了。接着我又和肖刘想出了D的算法,最后成功AC。期间李晔晨一直在调试E,未果。
本次比赛比较可惜的是,我们会G的算法,但是没有时间写了。而且I的算法也只差一点就想到了。时间不够用的原因就是代码能力不够,希望以后可以加强这方面的能力,再接再厉。
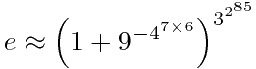
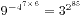 ,而e的极限形式是
,而e的极限形式是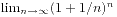 ,所以一切都可以解释了。
,所以一切都可以解释了。