Jan 17
完整的题目描述在这里。
题目给出了n和m,要求出满足最大公约数(x1,x2,...,xn,m)=1且xi不超过m的这样的x1,...,xn的组数。xi都是正整数。
如果n=1,那就是求欧拉函数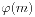 。我们可以联想其形式:
。我们可以联想其形式: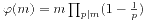 。那么当n>1时我们也来类比一下相对应的公式。
。那么当n>1时我们也来类比一下相对应的公式。
令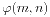 表示题目中所要求的答案。我们发现,当m为素数时,
表示题目中所要求的答案。我们发现,当m为素数时, 。这是显然的,因为除了(m,m,...,m,m)这一组数字以外,其余的都是可行的解。那么m不为素数时,我们把m的各个素因数分开考虑。如果某个素因数被n个数所共有,那么一共就少了
。这是显然的,因为除了(m,m,...,m,m)这一组数字以外,其余的都是可行的解。那么m不为素数时,我们把m的各个素因数分开考虑。如果某个素因数被n个数所共有,那么一共就少了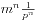 种方案,考察m所有的素因数,我们得到
种方案,考察m所有的素因数,我们得到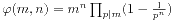 。
。
至此,问题解决。