Jan 11

求正整数集合使得元素之和等于元素之积

Art of Science 0 Comments

这是一个比较有意思的正整数性质的应用。我们应该可以迅速找到一个解{1,2,3}，但是如果要说明这个解的唯一性，我们需要做出一些讨论。

令这个集合为S={x1,...,xn}，这里n>1，0<x1<...<xn。 我们得到nx1<x1...xn<nxn，于是x1...xn-1<n，而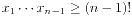$x_1\cdots x_{n-1}\geq (n-1)!$，所以n>(n-1)!>(n-1)(n-2)，解得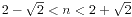$2-\sqrt{2}<n<2+\sqrt{2}$，于是n=2或3。又x1+...+xn=x1...xn， 解得n=2时x1=x2=2，舍弃，所以n=3，易解得x1=1,x2=2,x3=3。 问题得解。