Jan 18

NEERC2005 - Joseph

Art of Science 0 Comments

NEERC2005主页在这里。

题目给定n和k，要求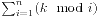$\sum_{i=1}^n(k\mod i)$。

我们先找一下规律，发现与等差数列是有关系的。我们对于当前的i，令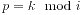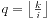$p=k\mod i$，$q=\left\lfloor\frac{k}{i}\right\rfloor$。那么当i增大1时，如果q不变，p一定减少了q，那么将p一直减小到0，同时对这一段进行求和（用数列求和公式），同时i增大到下一段的开头。

详细情况见代码：

#include <cstdio>
#include <algorithm>

using namespace std;

int n,k;

__int64 sum(int a,int d,int n) {
  return (__int64)(2*a-d*n)*(n+1)/2;
}

int main() {
  freopen("joseph.in","r",stdin);
  freopen("joseph.out","w",stdout);
  scanf("%d%d",&n,&k);
  int i = 1,p,q,a;
  __int64 r = 0;
  while (i<=n) {
    q = k%i; p = k/i;
    if (p>0) a = q/p;
    else a = INT_MAX;
    r += sum(q,p,min(a,n-i));
    i += min(a,n-i)+1;
  }
  printf("%I64d\n",r);
  return 0;
}