无限递降法
无限递降法就是一种特殊的反证法,它利用了最小自然数原理。先假设存在一个最小解,然后在这个最小解的基础上推出一个更小的解,再结合最小自然数原理得到矛盾,从而证明命题。
无限递降法经典的一个例子就是证明x4+y4=z2没有正整数解。
我们假定存在一个正整数解,那么其中必定存在一个解x0,y0,z0使得z0最小。我们得到必有(x0,y0)=1,否则会推出一个更小的解。由于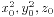 是方程x2+y2=z2的一个本原解,所以x0和y0必然是一奇一偶,不妨设2|y0,以及(y0,z0)=1。
是方程x2+y2=z2的一个本原解,所以x0和y0必然是一奇一偶,不妨设2|y0,以及(y0,z0)=1。
我们有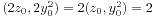 ,由此及2不整除
,由此及2不整除 即得
即得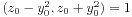 。我们又有
。我们又有
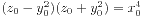
令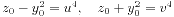 。这里v>u>0,(u,v)=1,u,v都是奇数。进而有
。这里v>u>0,(u,v)=1,u,v都是奇数。进而有
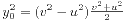
我们又得到(v2-u2,(v2+u2)/2)=1,因为(v2-u2,v2+u2)|(2v2,2u2)=2(v2,u2)=2,又u,v都是奇数,所以2不整除(v2+u2)/2,所以(v2-u2,(v2+u2)/2)=1。
我们再令v2-u2=a2,(v2+u2)/2=b2,这里a>0,b>0,(a,b)=1,2|a,2不整除b。由u,v满足的条件及a,b得0<b<v<z0,及u,a,v是方程x2+y2=z2的本原解且2|a。因此得到u=r2-s2, a=2rs, v=r2+s2。所以r4+s4=b2,而b<z0,与z0的最小性矛盾,命题得证。
无限递降法对于构造的要求很高,确实不是一个很好用的方法。
本作品遵循“署名-非商业性使用-相同方式共享 3.0 Unported”协议,转载请注明来自richard-desktop。

 评论 (0)
评论 (0)