这里的同余包含了同余和同余方程两个章节。

基本的同余概念可以从带余除法中推导出来。使用带余除法，我们可以得到同余式的相关运算性质。

接下来，我们引入同余类和剩余系的概念。剩余系主要是介绍了既约剩余系。我们从既约剩余系的定义中引出了Euler函数。Euler函数是一个积性函数，也就是说如果(m₁,m₂)=1，那么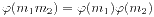。Euler函数有如下的计算式 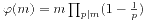，特别的，当m=p^k时，我们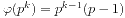有。我们还有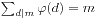，我们可以从中看出Mobius函数的一点影子。

接下来，我们由一个性质得到了一个重要的定理：Fermat-Euler定理。这个性质是，对于一个模m，它的任何一个既约剩余系中所有元素的乘积模m是相同的，也可以表述为(a,m)=1时，x遍历m的既约剩余系当且仅当ax遍历m的既约剩余系。我们得到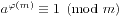，以及当m=p时，对于任意的a，我们有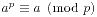。前面的式子被称为Fermat小定理，后面的式子被称为Euler定理。

Wilson定理是如下的内容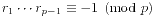，也就是对于一个素数p>3，它的既约剩余系中所有数的乘积模p为-1。特别的，我们有。事实上，p不取1,2,4,p^k,2p^k时，p的既约剩余系的积模p得1。Wilson虽然不能用来高效地检验素数，但是可以被用来简化运算。

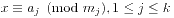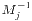同余方程是多项式同余的形式。其最简单的形式是一次同余方程。我们可以用带余除法和辗转相除法得到其解。中国剩余定理用来求解一次同余方程组。对于一个一次同余方程组，这里m₁,...,m_k两两既约。那么其解为，m=m₁...m_k，m=m_jM_j，以及是M_j模m_j的逆。这个解的正确性容易带入验证。如果m₁,...,m_k并非两两既约，则可以化为各个方程都是模p^k的形式更加方便。

关于模为素数的二次同余方程，我们只需要讨论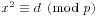的形式。对于模p，如果一个d能使得方程有解，那么我们称d为模p的二次剩余；否则d就是模p的二次非剩余。我们可以用Euler判别法来进行判断。如果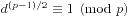，那么d就是模p的二次剩余；如果，那么d就是模p的二次非剩余。

我们还可以引进Legendre符号和Jacobi符号来进行进一步的研究。Gauss二次互反律也是进一步的探讨对象。具体内容可以参见原书或者nmbr.rar。

• Relative Posts