一上来作者介绍了Peano公理。这个公理告诉我们，自然数就是一个有起点的、存在后继的无限整数集合。自然数的性质都可以通过这个抽象的定义来推导。我们一般使用1,2,3,...，是因为它本身具有代表性。至于0的问题，一般在不涉及的情况下不考虑。从Peano公理我们得到了数学归纳法和两个自然数的原理：最小和最大自然数原理。数学归纳法在数论当中可以用来证明多项的命题，也可以用来证明取值范围是固定连续整数域的恒等式或者命题。

接下来是整除的概念，我们一般是把它和带余除法结合起来看。从基本定义我们就可以推导很多有用的性质。从整除我们得到一类非常有用的数：素数。素数具有很多的性质。关于素数的判定也是一个很重要的课题，一般而言我们有试除法、Fermat素性检验、Miller-Rabin素性检验。A.K.S算法是第一个被证明的可以在多项式时间内检验素数的算法。

接下来作者介绍了公约数和公倍数的理论。我们又得到了互素的概念。这在书中仅仅是一个先头的简单介绍，作者接着引进了带余除法的概念。这是一个非常有用的概念，我们可以通过它进行很多讨论余数的证明。整数分类也是来自于带余除法。有了带余除法的概念之后，我们就可以讨论很多情况下余数的性质。带余除法是初等数论中极其重要的内容。

接下来就是辗转相除法。这也是一个来自于带余除法的内容。

我们现在可以建立最大公约数理论。带余除法、辗转相除法和整系数线性组合是3种很容易被引进的方法。我们需要了解的是，一个集合中数的最大公约数就是这些数的整系数线性组合中最小的那一个，也就是。

现在进入到了算术基本定理，我们现在可以用素数的性质来对整数进行分析。由于算术基本定理的存在，我们一定可以通过分析素数的性质来得到相关整数的性质。这里需要介绍一下除数和函数。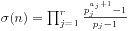

对于本章最后的[x]函数的分析，就不再过多的叙述，因为都是很普通的内容。而对于n!的分解式，要能够体会其中蕴含的缩小规模的递归思想。

最后是容斥原理和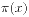的分析。容斥原理更多的是使用在组合数学当中。而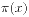的计算需要相应的推导，具体内容可以参见书中。或者可以参见我的另外一个笔记：nmbr.rar。

• Relative Posts