SWERC2008 Solutions

张文泰 posted @ 2010年1月15日 02:23 in Art of Science with tags SWERC acm , 3396 阅读

SWERC2008主页在这里：SWERC 2008 - Nuremberg。这套题目还是一贯的欧洲赛区的风格，题目大多数都可以做。

Bring Your Own Horse：题目很长很烦，从最后的Scoreboard就可以看出来很多人因为题目描述的原因没有看出来题目的意思。题目的要求很简单，就是先求一个最小生成树，然后对于每一个询问，都用一次BFS来找到生成树中两点之间路径当中最长的边。代码量并不大，但是最快的提交也用了66分钟，完全是题目描述的问题。
First Knight：一个非常明显的高斯消元法，如果在中国赛区应该算是容易的。

Postal Charges：一个别出心裁的降低复杂度的题目。巧妙的用类似桶排序的方法先进行分类，然后考虑到只是进行曼哈顿距离的计算，所以可以分块求解。每一个块中不同的元素都已经预处理出到自身所在块的左下角的距离，使用乘法原理就可以解决。

double calc() {
  double sum = 0.0; //总长度
  int co = 0;       //路线数量
  for (int i = 1; i<MAX; i++)
    for (int j = 1; j<MAX; j++) //i,j枚举当前的块
      for (int k = 0; k<i; k++)
        for (int l = 0; l<j; l++) { //k,l枚举当前快之前的块
          //l[i][j]表示(i,j)这个块里面所有点的该块左下角的距离之和
          //c[i][j]表示每个块中含有元素的个数
          sum += l[i][j]*c[k][l]-l[k][l]*c[i][j]+(i-k+j-l)*c[i][j]*c[k][l]; //乘法原理
          co += c[i][j]*c[k][l]; //求和
        }
  return sum/co;
}

Randomly-priced Tickets：题目给定了一个无向图。首先用Floyd求出两点之间的距离，然后就是要求在一条定长的路线上分配初始的预算。这个问题用动态规划很容易解决。设p(i,j)表示长度为i的路线，预算为j，能够通过的可能性，那么 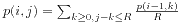$p(i,j)=\sum_{k\geq 0,j-k\leq R}\frac{p(i-1,k)}{R}$ ，边界条件是i=0时p(i,j)=1。如果一个询问的两点之间长度为d，预算为b，直接输出p(d,b)就可以了。
The Game：博弈问题，用最大最小搜索，Alpha-Beta剪枝应该会有好的效果。
The Merchant Guild：动态规划。首先要确定方案合法的充要条件，就是最多不超过i个商人被分配到了最后的n-i+1个位置。这样令f(k,m)为在k,...,n之间还有m个空位时的分配方案数，s(k)表示前k个位置一共有多少本地商人，g(k,m)=m+1-s(k-1)+s(k-2)，那么
$\displaystyle f(k,m)=\sum_{i=0}^{g(k,m)}{{k-s(k-1)+m}\choose {g(k,m)-i}}f(k-1,i)$
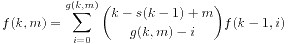
Toll Road：分治。题目所给的是一个树，只要DFS一次，找出最大权值的子树就可以了，用分治法会很轻松。
Top Secret：矩阵乘法。我们依据题意构造出矩阵之后进行计算，由于这是一个循环矩阵，可以把O(n³)的算法优化至O(n²)。
Transcribed Books：数论题。注意到对于所有的序列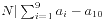， $N|\sum_{i=1}^9 a_i -a_{10}$ 。那么所有序列的 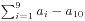$\sum_{i=1}^9 a_i-a_{10}$ 的最大公约数在有解的情况下就是问题的答案。
Wizards：数学题。详细情况请参见判断方程是否有重根。