Feb 24

戴德金分割理论（Dedekind Cut）

Art of Science 1 Comments

对于实数集这个概念，我们有一些很好的基本性质：

  • 实数集是一个有序集；
  • 实数集是稠密的；
  • 实数集中四则运算具有封闭性。

当然，这些性质并不能严格地给出实数的定义，戴德金分割理论正是为此而产生的一个理论。

戴德金理论是一种对集合进行划分的方法。前提是这个集合是可以严格排序的。方法把待分割的集合分成两个交集为空且自身不为空的集合A和B，而且A中的任何元素都比B中的元素小。我们令全集为U，那么形式化的：

  • $A\cup B=U$；
  • $A\cap B=\phi$，$A,B\neq \phi$；
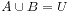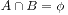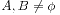  • 对于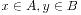$x\in A,y\in B$，必然有x<y。

显然，对于A和B中最大值和最小值的情况有四种情况。

首先，整数集、有理数集、实数集都是存在戴德金分割的。对于整数集来说，由于不存在稠密性，分割中A必定存在最大值，B必定存在最小值。我们可以把相应的最值称为边界数。而对于有理数集和实数集而言，要么A中存在最大值，要么B中存在最小值，必定满足且仅满足其中的一个。这很容易证明，如果同时满足，那么根据有理数集和实数集的稠密性，两个边界数中必定还存在一个既不属于A又不属于B的数，与分割的定义矛盾。

所以我们可以根据有理数集的戴德金分割来定义实数集。

对于有理数集Q的一个戴德金分割，如果A中存在最大值或者B中存在最小值，那么就定义了一个有理数；如果A中没有最大值，B中也没有最小值，那么就定义了一个无理数。实际上，分割的情况不外乎下面三种：

  • $A=\{x<r\},B=\{x\geq r\}$；
  • $A=\{x\leq r\},B=\{x>r\}$；
  • $A=\{x<r\},B=\{x>r\}$。

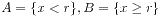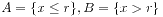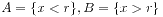前面两种情况就定义了有理数r，最后一种情况则定义了无理数r。之所以会有这种区别，是因为实数集具有连续性。

如果我们规定有理数集的戴德金分割不允许集合A有边界数，那么可以建立分割和实数的一一对应关系，在有理数的基础上定义了实数，这为数学分析奠定了基础。