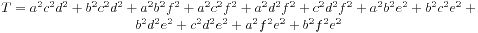richard-desktop

这道题看上去有点欧几里得算法的意思在里面，实际上不是。我仅仅是在判断有没有解的时候用了一次求最大公约数的算法，接下来就是模拟，分别模拟从a往b倒和从b往a倒得两种情况，很容易就Accepted了。 

#include <cstdio>
#include <climits>

using namespace std;

int ntest,a,b,c,d;

int min(int a,int b) {
    return a<b?a:b;
}

int gcd(int a,int b) {
    return b==0?a:gcd(b,a%b);
}

int check(int a,int b) {
    int ret = 0,ca = 0,cb = 0;
    for (;;) {
        if (ca==c || cb==c) return ret;
        if (cb==b) cb = 0;
        else if (ca==0) ca = a;
        else {
            int dt = min(b-cb,ca);
            ca -= dt; cb += dt;
        }
        ret++;
    }
}

int main() {
    scanf("%d",&ntest);
    while (ntest--) {
        scanf("%d%d%d",&a,&b,&c);
        d = gcd(a,b);
        if (c%d!=0 || c>a && c>b) printf("-1\n");
        else {
            int ans = check(a,b);
            ans = min(ans,check(b,a));
            printf("%d\n",ans);
        }
    }
    return 0;
}

Your program in C++ from 2010-04-09 07:16:22 ran for 0.01 seconds and used 2536 KB of memory.

这个题目相当经典了，是一个树结构的询问题。一般而言，这种题目都是先给出一个树，然后进行更改边权值、对边的修改（节点也可以），然后对某段路径进行询问。从根本上来讲，这类题目的本质都是在维护树的路径。

QTREE算是这类题目中的一道入门题。给出一棵树，然后更改边的权值或者询问一条路径上边权最大的边。由于不涉及树的形态，我们直接用树链剖分先构造固定的线段树来维护路径。对于相应的更改和询问，只要先预处理好LCA就可以轻松维护了。

在树中不同路径中遍历的复杂度是O(log n)，查询一次边的复杂度是O(log n)，每次查询LCA的复杂度是O(log n)。我在预处理LCA的时候采用的是O(n log n)-O(log n)的算法，所以总的复杂度就是O(n log n+q log² n)。事实上，如果我们用RMQ的O(n)-O(1)算法来处理这个LCA，复杂度就应该是O(n+qlog² n)。

值得注意的是，使用gets()优化一下输入，程序会快很多，我的程序就快了1.37s。至于为什么我的程序这么慢，只能说明我的代码写得太烂了。

Your program in C++ from 2010-04-07 07:19:34 ran for 4.09 seconds and used 4424 KB of memory.

Your program in C++ from 2010-04-07 11:05:42 ran for 2.72 seconds and used 4348 KB of memory.

题目要求我们时刻维护一个数列的逆序对个数，n在250000的范围内。虽然可能出现的数字总数只有60000（=50000+10000），但是仍然是一个让人头疼的问题。

对于不需要更改的问题，我们可以用多种方法求出其答案。加入了更改操作之后，我们需要维护相关的内容来更新这个值。

我们回忆块状链表的内容，可以配合做出相应的改变。比如，一开始我们用树状数组（Binary Indexed Trees）求逆序对，那么可以产生相应的块状树状数组。我们通过分块维护来降低维护的费用。

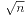这样一来问题就变得比较简单了。需要说明的是，具体编写程序的时候需要在的基础上加权分块，不然会出现TLE的问题。

题目的意思很明确，就是要求出一组绝对值函数的最小值。由于规模较大，我们要找出一个n²以下复杂度的算法。

对于一般的绝对值求最值问题，我们首先想到的是把绝对值的符号打开，然后再加以讨论。这个题目也不外如是。打开绝对值符号之后，我们发现，如果在i和j中能够确定一个值，那么就变成了一个查找最优值的问题。

我们如果能够确定i，那么加上确定了|x_j-x_i-1|+|x_j-x_i+1|两者的符号，我们就可以确定x_j的范围。这时候，我们还是没有办法直接找到最小值的。这是因为|x_i-x_j-1|+|x_i-x_j+1|的存在，使得x_j-1和x_j+1的取值也受到了限制。我们可以想办法把这个限制给去掉。

显然我们需要合理地安排查询顺序。由于绝对值符号展开后，我们可以得到最值的表达式，对于不同的i，我们都能构造出关于j的函数使得这些函数都能够适用。也就是说，产生一个关于j的函数，使得查找变成求这个函数的最值，就可以求出问题的最值。

我们要想办法把这个关于j的函数的最值转化为在某个范围内求最值的问题。通常想到的就是区间查询问题。这里我们需要避免高维的区间查找情形。

我们考察所有式子展开的情况。如果|x_i-x_j-1|+|x_i-x_j+1|的符号都是正，那么x_i的范围就是大于x_j-1和x_j+1的较大值，这样，我们把xj按照x_j-1和x_j+1的较大值从小到大排序，同时如果查找也是按照x_i从小到大的顺序进行，那么就可以用两个指针维护查找过程，达到O(n)的外循环复杂度，而且不会与条件冲突，同时建立一维线段树，按照|x_j-x_i-1|+|x_j-x_i+1|的符号进行相关区间的最值查找。

如果|x_i-x_j-1|+|x_i-x_j+1|的符号都是负，也是差不多的情形。需要商榷的就是x_i在x_j-1与x_j+1之间的情况。这时，我们可以把它们看成一个区间[x_j-1, x_j+1]，把这些区间按照一定顺序排序，再通过这些区间来确定i的范围，再来完成查找就可以了。这里需要判断某个i会在哪些区间中，这样，查找一个i的复杂度就是O(log² n)。这里需要借鉴这里的数据结构：2D de aici。

由于只有最后一种情况的单次查找复杂度是O(log² n)，我们得到的算法复杂度是O(nlog² n)。绝对值打开之后一共有8种情况，我们需要逐一讨论，相当繁琐。

题目要求四面体的内接球半径。因为数据都是以大整数的形式给出，单纯的解析法精度不能满足要求。由于V=RS/3，所以我们只要求出V（体积）和S（表面积），依然可以求出R。

四面体的体积在已知6条边的长度的时候是可以通过公式进行计算的。设6条边长度分别为a, b, c, d, e, f，而且(a, f)，(b, e)，(c, d)不共面，那么体积为：

公式可以去查看大图。这样问题就很容易了。

#include <cstdio>
#include <cmath>

using namespace std;

double a,b,c,d,e,f;

#define s(x) (x*x)

double t(double a,double b,double c) {
  double p = (a+b+c)/2;
  return sqrt(p*(p-a)*(p-b)*(p-c));
}

int main() {
  int ncase;
  scanf("%d",&ncase);
  while (ncase--) {
    scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f);
    double v = s(a*b*e)+s(a*b*f)+s(a*c*d)+s(a*c*f)+s(a*d*f)+s(a*f*e)
              +s(b*c*d)+s(b*c*e)+s(b*d*e)+s(b*f*e)+s(c*d*e)+s(c*d*f)
              -s(a*b*d)-s(a*c*e)-s(b*c*f)-s(d*e*f)
              -s(c*c*d)-s(c*d*d)-s(a*a*f)-s(a*f*f)-s(b*b*e)-s(b*e*e);
    v = sqrt(v)/12;
    double s = t(a,b,d)+t(a,c,e)+t(b,c,f)+t(d,e,f);
    printf("%.4f\n",v/s*3);
  }
  return 0;
}

Your program in C++ from 2010-03-20 04:57:43 ran for 0.00 seconds and used 2536 KB of memory.