SPOJ 16 - Sphere in a tetrahedron[TETRA]

张文泰 posted @ 2010年3月20日 20:10 in Art of Science with tags SPOJ 四面体 , 3847 阅读

题目要求四面体的内接球半径。因为数据都是以大整数的形式给出，单纯的解析法精度不能满足要求。由于V=RS/3，所以我们只要求出V（体积）和S（表面积），依然可以求出R。

四面体的体积在已知6条边的长度的时候是可以通过公式进行计算的。设6条边长度分别为a, b, c, d, e, f，而且(a, f)，(b, e)，(c, d)不共面，那么体积为：

$T=a^2c^2d^2+b^2c^2d^2+a^2b^2f^2+a^2c^2f^2+a^2d^2f^2+c^2d^2f^2+a^2b^2e^2+b^2c^2e^2+b^2d^2e^2+c^2d^2e^2+a^2f^2e^2+b^2f^2e^2$

$V=\frac{\sqrt{T-a^2b^2d^2-a^2c^2e^2-b^2c^2f^2-d^2f^2e^2-c^4d^2-c^2d^4-a^4f^2-a^2f^4-b^4e^2-b^2e^4}}{12}$

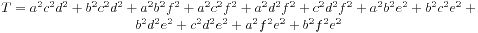
公式可以去查看大图。这样问题就很容易了。

#include <cstdio>
#include <cmath>

using namespace std;

double a,b,c,d,e,f;

#define s(x) (x*x)

double t(double a,double b,double c) {
  double p = (a+b+c)/2;
  return sqrt(p*(p-a)*(p-b)*(p-c));
}

int main() {
  int ncase;
  scanf("%d",&ncase);
  while (ncase--) {
    scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f);
    double v = s(a*b*e)+s(a*b*f)+s(a*c*d)+s(a*c*f)+s(a*d*f)+s(a*f*e)
              +s(b*c*d)+s(b*c*e)+s(b*d*e)+s(b*f*e)+s(c*d*e)+s(c*d*f)
              -s(a*b*d)-s(a*c*e)-s(b*c*f)-s(d*e*f)
              -s(c*c*d)-s(c*d*d)-s(a*a*f)-s(a*f*f)-s(b*b*e)-s(b*e*e);
    v = sqrt(v)/12;
    double s = t(a,b,d)+t(a,c,e)+t(b,c,f)+t(d,e,f);
    printf("%.4f\n",v/s*3);
  }
  return 0;
}