最短增广路，顾名思义，就是一条增广路，而且还是所有增广路中最短的一条。要求出最短增广路也十分容易，只要在残量网络中求出源点到汇点的最短路就可以了（所有边的长度为1）。
求出了最短增广路，我们就可以沿着它对网络进行增广，而且可以证明，如果只要求最大流，最多经过n（n为总结点数）次增广，就可以求出最大流。实现也非常简单，由于所有边的长度为1，所以只需要使用宽搜。使用最短增广路的方法求最大流，其实也是Ford-Fulkerson方法的一种，这种方法的特点是每次找出一条残量网络中的增广路径并进行增广。整个过程中满足流的网络的三个性质：容量限制、反对称性、流守恒性。
如果不知道什么是残量网络（或者又被叫做残留网络），请看下面的解释。
- 残量：容量－流量。
- 残留边：有残留容量的边成为残留边
- 残留网络：由网络的点集、残留边集构成残留网络。
这里我们需要注意一点，宽搜的结果如果可以为后面所利用的话，我们就可以写出一种新的求最大流的算法：SAP，全称Shortest Augmenting Path Algorithm。其时间复杂度为O(n2m)。在实践中，这种算法效率还是比较高的，而且性价比相当好（我一般都会使用它）。
在SAP中，定义每个点的距离标号，即残留网络中点到汇点的距离。然后，只需要在距离标号相邻的点间寻找增广路径。如果从一个点出发没有可行边，就对该点进行重标记，然后并回溯（类似预流推进算法）。
可行边就是说，存在一条边<i,j>，当且仅当ri,j>0且di=dj+1时，边是容许边，我们的算法只考虑容许边（这里d指距离标号，r指残量网络中的流量）。
算法的一开始，我们从汇点t进行一次宽搜求出距离标号（或者也可以不进行预处理，直接赋值为0，因为随着重标记的过程，距离标号会自行调整），然后从源点s开始递归操作（或者也可以不递归，因为算法本身并不繁琐）。对于一个点i，如果存在容许边<i,j>，当j是汇点时增广并从源点开始递归，否则就令i是j的前驱，并递归j。否则对i重标号，使得di=min{dj|ri,j>0}+1，并回溯。当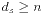
时算法停止，此时不存在任何一条增广路。
当然我们可以参考预流推进，对它进行间隙优化。同时还有一个叫做当前弧的优化，采用后速度也有一定的提升。而且，采用前向星的储存方式会更好。
我们也可以用最短增广路来求最小费用最大流，原理不需要再阐述了，如果是用增广路算法来求最小费用最大流，就是要找一条费用最少的路径来进行增广。当然可以套用最短增广路的方法来做。