richard-desktop

题目就是要求最短路，我们根据数据规模采用Dijkstra+Heap的算法。这里C++如果使用STL中的堆是没有办法过的。

#include <cstdio>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>

using namespace std;

const int MAXN = 10000+5;

typedef pair<int,int> pii;
typedef pair<string,int> psi;
typedef vector<pii>::iterator iter;

vector<pii> road[MAXN];
vector<psi> city;
int n,dis[MAXN],size;
int heap[MAXN],hash[MAXN];

inline void trylo(int u) {
  int tmp = heap[u],i = u;
  while (i*2+1<size) {
    int j = i*2+1;
    if (dis[heap[j+1]]<dis[heap[j]]) j++;
    if (dis[heap[j]]<dis[tmp]) {
      heap[i] = heap[j];
      hash[heap[i]] = i;
      i = j;
    }
    else break;
  }
  heap[i] = tmp;
  hash[heap[i]] = i;
}

inline void tryhi(int u) {
  int tmp = heap[u],i = u;
  while (i>0) {
    int j = (i-1)/2;
    if (dis[tmp]<dis[heap[j]]) {
      heap[i] = heap[j];
      hash[heap[i]] = i;
      i = j;
    }
    else break;
  }
  heap[i] = tmp;
  hash[heap[i]] = i;
}

inline void push(int u) {
  heap[size] = u; hash[u] = size++;
  tryhi(size-1);
}

inline int htop() {
  int ret = heap[0];
  hash[heap[0]] = -1;
  heap[0] = heap[size-1];
  hash[heap[0]] = 0;
  size--;
  trylo(0);
  return ret;
}

int dijkstra(int x,int y) {
  memset(dis,127,sizeof(dis));
  dis[x] = 0;
  size = 0;
  memset(hash,-1,sizeof(hash));
  push(x);
  while (size) {
    int u = htop();
    for (iter i = road[u].begin(); i!=road[u].end(); ++i) {
      int v = i->second;
      if (dis[v]>dis[u]+i->first) {
        dis[v] = dis[u]+i->first;
        if (hash[v]==-1) push(v);
        else tryhi(hash[v]);
      }
    }
  }
  return dis[y];
}

int main() {
  int ncase;
  scanf("%d",&ncase);
  while (ncase--) {
    scanf("%d",&n);
    city.clear();
    for (int i = 0,m; i<n; i++) {
      char _name[16];
      scanf("%s%d",_name,&m);
      city.push_back(psi(string(_name),i));
      road[i].clear();
      for (int j = 0,t,c; j<m; j++) {
        scanf("%d%d",&t,&c); t--;
        road[i].push_back(pii(c,t));
      }
    }
    sort(city.begin(),city.end());
    int query;
    scanf("%d",&query);
    while (query--) {
      char _na[16],_nb[16];
      scanf("%s%s",_na,_nb);
      int ia = lower_bound(city.begin(),city.end(),psi(string(_na),0))->second;
      int ib = lower_bound(city.begin(),city.end(),psi(string(_nb),0))->second;
      printf("%d\n",dijkstra(ia,ib));
    }
  }
  return 0;
}

Your program in C++ from 2010-03-20 04:16:58 ran for 2.66 seconds and used 7020 KB of memory.

• 1 - Life, the Universe, and Everything[TEST]
  模拟题，只需要按照要求做就可以了。
• 2 - Prime Generator[PRIME1]
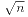  先用筛法求出范围内的质数，然后对指定的区间再使用筛法就可以了。不需要特别的优化。
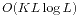• 4 - Transform the Expression[ONP]
  中缀转后缀，经典问题，用栈操作就可以了。
• 5 - The Next Palindrome[PALIN]
  只需要提取出前半部分，然后累加再判断是否符合要求就可以了。
• 6 - Simple Arithmetics[ARITH]
  注意到水平线的长度只和直接相邻的上下两行有关。
• 8 - Complete the Sequence![CMPLS]
  见SPOJ 8 - Complete the Sequence![CMPLS]。
• 10 - Complicated Expressions[CMEXPR]
  利用中缀转后缀的结果进行去括号是比较稳妥的做法。分析表达式树也是可行的。
• 11 - Factorial[FCTRL]
  简单题。
• 14 - I-Keyboard[IKEYB]
  见SPOJ 14 - I-Keyboard[IKEYB]。
• 15 - The Shortest Path[SHPATH]
  见SPOJ 15 - The Shortest Path[SHPATH]。
• 16 - Sphere in a tetrahedron[TETRA]
  见SPOJ 16 - Sphere in a tetrahedron[TETRA]。
• 22 - Triangle From Centroid[TRICENTR]
  平面几何题。我们先求出基本的三边长、三条高的长度。然后，建立坐标系，算出外心的坐标。由欧拉线的性质可知，重心到外心的距离是重心到垂心距离的一半，所以可以得到答案。
• 23 - Pyramids[PIR]
  与TETRA一题方法一样。
• 24 - Small factorials[FCTRL2]
  简单题。
• 25 - Pouring water[POUR1]
  见SPOJ 25 - Pouring water[POUR1]。
• 27 - Sorting Bank Accounts[SBANK]
  就是简单的排序，用gets()应该可以保证不会超时。
• 29 - Hash it![HASHIT]
  Hash表的简单应用。
• 31 - Fast Multiplication[MUL]
  高精度乘法，可以使用FFT等算法。其实直接压位也可以过。
• 32 - A Needle in the Haystack[NHAY]
  KMP算法就可以过了。不过如果按照题目中给的提示，采用动态内存分配程序似乎有点慢。
• 33 - Trip[TRIP]
  动态规划，没什么难度。
• 39 - Piggy-Bank[PIGBANK]
  背包问题，动态规划解决之。
• 40 - Lifting the Stone[STONE]
  求多边形的重心，一般采用三角剖分做，剖分的中心点往往是原点。
• 42 - Adding Reversed Numbers[ADDREV]
  简单题。
• 54 - Julka[JULKA]
  简单题。
• 375 - Query on a tree[QTREE]
  见SPOJ 375 - Query on a tree[QTREE]。
• 861 - Counting inversions[SWAPS]
  见SPOJ 861 - Counting inversions[SWAPS]。
• 1644 - Trees[TREEOI14]
  见SPOJ 1644 - Trees[TREEOI14]。

动态规划。我们先预处理出必要的区间段信息，然后发现其满足单调性，于是采用单调性优化。我们使用的是f(x)=min{f(i)+w(i,x)}这一经典模型，二分求出决策就可以了，总的复杂度是。

#include <cstdio>
#include <climits>
#include <cstring>
#include <stack>

using namespace std;

const int MAXN = 90+5;

struct status {
  int u,b,e;
  status(int _u,int _b,int _e)
    : u(_u),b(_b),e(_e) {}
  status() {}
};

char ma[MAXN],mb[MAXN];
int n,m,f[MAXN][MAXN],w[MAXN];
int p[MAXN][MAXN],r[MAXN],g[MAXN][MAXN];
stack<status> st[MAXN];
int tdec[MAXN];

int main() {
  int ncase;
  scanf("%d",&ncase);
  for (int loop = 1; loop<=ncase; loop++) {
    scanf("%d%d",&m,&n);
    scanf("%s%s",ma,mb);
    for (int i = 1; i<=n; i++)
      scanf("%d",&w[i]);
    for (int i = 1; i<=n; i++) {
      g[i][i] = w[i];
      for (int j = i+1; j<=n; j++)
        g[i][j] = g[i][j-1]+w[j]*(j-i+1);
    }
    f[0][0] = 0;
    st[1].push(status(1,1,n));
    for (int i = 1; i<=m; i++) {
      while (!st[i].empty()) {
        status tmp = st[i].top();
        for (int j = tmp.b; j<=tmp.e; j++)
          p[i][j] = tmp.u;
        st[i].pop();
      }
      for (int j = i; j<=n; j++)
        f[i][j] = f[i-1][p[i][j]-1]+g[p[i][j]][j];
      if (i<m) {
        st[i+1].push(status(i+1,i+1,n));
        for (int j = i+2; j<=n; j++) {
          while (!st[i+1].empty()) {
            int u = st[i+1].top().u;
            int b = st[i+1].top().b;
            if (j<=b && f[i][u-1]+g[u][b]>f[i][j-1]+g[j][b])
              st[i+1].pop();
            else break;
          }
          int u = st[i+1].top().u;
          int e = st[i+1].top().e;
          if (j<=e && f[i][u-1]+g[u][e]>f[i][j-1]+g[j][e]) {
            int l = st[i+1].top().b,r = e; // (]
            while (l+1<r) {
              int mid = (l+r)/2;
              if (j<=mid && f[i][u-1]+g[u][mid]>f[i][j-1]+g[j][mid]) r = mid;
              else l = mid;
            }
            st[i+1].top().e = l;
            st[i+1].push(status(j,l+1,n));
          }
          else if (e+1<=n) st[i+1].push(status(j,e+1,n));
        }
      }
    }
    for (int i = m,j = n; i>0; i--) {
      r[i] = p[i][j];
      j = r[i]-1;
    }
    r[m+1] = n+1;
    printf("Keypad #%d:\n",loop);
    for (int i = 1; i<=m; i++) {
      printf("%c: ",ma[i-1]);
      for (int j = r[i]; j<r[i+1]; j++)
        printf("%c",mb[j-1]);
      printf("\n");
    }
    printf("\n");
  }
  return 0;
}

Your program in C++ from 2010-03-19 08:54:48 ran for 0.53 seconds and used 2792 KB of memory.

题目给出了一个数列的前若干项，要求推测后面的项。我们很容易想到拉格朗日插值法，但是精度就变成了一个大问题。这个问题虽然保证了所有的值都是整数，但是并没有保证其多项式的系数也是整数，因此在计算方面存在很大的困难。

除了插值法，求解这种数列问题我们有更好的差分方法，过程中完全不涉及浮点数操作。比如说，对于1 2 4 7 11 16 22 29这个数列，我们对于每一项做其和前一项的差，也就是2-1=1, 4-2=2, 7-4=3, ....这样，我们得到一个1阶差分：1, 2, 3, 4, 5, 6, 7。我们再求得2阶差分是：1, 1, 1, 1, 1, 1。这时，规律已经有些明显了。

也就是说，对于任意一个存在合理多项式通项的数列，用差分的方法是可以得到它的解的：只要求得这个n项数列的n-1阶差分，然后倒推回去就可以了。代码如下：

#include <cstdio>
#include <cstring>

using namespace std;

const int MAXN = 100+5;

int n,m,s[MAXN][MAXN];

int main() {
  int ncase;
  scanf("%d",&ncase);
  while (ncase--) {
    scanf("%d%d",&n,&m);
    for (int i = 0; i<n; i++)
      scanf("%d",&s[0][i]);
    for (int i = 1; i<n; i++)
      for (int j = 0; i+j<n; j++)
        s[i][j] = s[i-1][j+1]-s[i-1][j];
    for (int i = 1; i<=m; i++)
      s[n-1][i] = s[n-1][0];
    for (int i = n-2; i>=0; i--)
      for (int j = 0; j<m; j++)
        s[i][n-i+j] = s[i][n-i+j-1]+s[i+1][n-i+j-1];
    for (int i = 0; i<m-1; i++)
      printf("%d ",s[0][n+i]);
    printf("%d\n",s[0][n+m-1]);
  }
  return 0;
}

Your program in C++ from 2010-03-18 12:22:31 ran for 0.52 seconds and used 2576 KB of memory.