SPOJ 14 - I-Keyboard[IKEYB]

张文泰 posted @ 2010年3月20日 00:07 in Art of Science with tags SPOJ 动态规划 , 3049 阅读

动态规划。我们先预处理出必要的区间段信息，然后发现其满足单调性，于是采用单调性优化。我们使用的是f(x)=min{f(i)+w(i,x)}这一经典模型，二分求出决策就可以了，总的复杂度是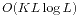 $O(KL\log L)$ 。

#include <cstdio>
#include <climits>
#include <cstring>
#include <stack>

using namespace std;

const int MAXN = 90+5;

struct status {
  int u,b,e;
  status(int _u,int _b,int _e)
    : u(_u),b(_b),e(_e) {}
  status() {}
};

char ma[MAXN],mb[MAXN];
int n,m,f[MAXN][MAXN],w[MAXN];
int p[MAXN][MAXN],r[MAXN],g[MAXN][MAXN];
stack<status> st[MAXN];
int tdec[MAXN];

int main() {
  int ncase;
  scanf("%d",&ncase);
  for (int loop = 1; loop<=ncase; loop++) {
    scanf("%d%d",&m,&n);
    scanf("%s%s",ma,mb);
    for (int i = 1; i<=n; i++)
      scanf("%d",&w[i]);
    for (int i = 1; i<=n; i++) {
      g[i][i] = w[i];
      for (int j = i+1; j<=n; j++)
        g[i][j] = g[i][j-1]+w[j]*(j-i+1);
    }
    f[0][0] = 0;
    st[1].push(status(1,1,n));
    for (int i = 1; i<=m; i++) {
      while (!st[i].empty()) {
        status tmp = st[i].top();
        for (int j = tmp.b; j<=tmp.e; j++)
          p[i][j] = tmp.u;
        st[i].pop();
      }
      for (int j = i; j<=n; j++)
        f[i][j] = f[i-1][p[i][j]-1]+g[p[i][j]][j];
      if (i<m) {
        st[i+1].push(status(i+1,i+1,n));
        for (int j = i+2; j<=n; j++) {
          while (!st[i+1].empty()) {
            int u = st[i+1].top().u;
            int b = st[i+1].top().b;
            if (j<=b && f[i][u-1]+g[u][b]>f[i][j-1]+g[j][b])
              st[i+1].pop();
            else break;
          }
          int u = st[i+1].top().u;
          int e = st[i+1].top().e;
          if (j<=e && f[i][u-1]+g[u][e]>f[i][j-1]+g[j][e]) {
            int l = st[i+1].top().b,r = e; // (]
            while (l+1<r) {
              int mid = (l+r)/2;
              if (j<=mid && f[i][u-1]+g[u][mid]>f[i][j-1]+g[j][mid]) r = mid;
              else l = mid;
            }
            st[i+1].top().e = l;
            st[i+1].push(status(j,l+1,n));
          }
          else if (e+1<=n) st[i+1].push(status(j,e+1,n));
        }
      }
    }
    for (int i = m,j = n; i>0; i--) {
      r[i] = p[i][j];
      j = r[i]-1;
    }
    r[m+1] = n+1;
    printf("Keypad #%d:\n",loop);
    for (int i = 1; i<=m; i++) {
      printf("%c: ",ma[i-1]);
      for (int j = r[i]; j<r[i+1]; j++)
        printf("%c",mb[j-1]);
      printf("\n");
    }
    printf("\n");
  }
  return 0;
}