骑士周游是指在一个N×M的棋盘上,从某一点出发,按照国际象棋的跳法,不重复地经过每一个格子。其实本质上是求一个Hamilton回路。我们有时候需要对给定的一个棋盘,输出一个骑士周游的方案。往往首先想到的是搜索。但是搜索对于N,M较大的时候并不可取,这时候就会想到构造。我所了解的构造方法有两种,一种是在小棋盘的基础上每次增加宽度为2的路径,一种是把4个小棋盘合并起来。这里所要介绍的是后一种方法。而且这两种构造方法都对N,M有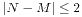 且均为偶数的要求。
且均为偶数的要求。
首先,考虑N×N的棋盘。对棋盘进行黑白染色,得出马的路径必然是黑白相间的这一结论。又由于一条Hamilton回路上的黑白格子的数量应当相等,所以在N×N为奇数的时候问题无解。也就是在N为奇数的时候无解。反之,在N为偶数的情况下,一定存在Hamilton回路。
首先观察一下最基本的棋盘。由于4×4的棋盘无解,所以在这里我们只考虑6×6、6×8、8×8、 8×10、10×10、10×12的棋盘。据有关资料说,对于这些棋盘用回溯法可以在O(1)的时间内找到Hamilton回路,但是具体情况我不清楚。对于4个角上的格子,由于它们的度仅为2,而且观察有解的情况,必定是下面的情况。
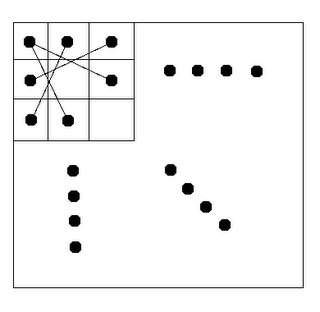
而如果要得到8×6、10×8、12×10,只需要将6×8、8×10、10×12的棋盘旋转90度。对于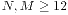 的情形,我们就需要采用分治策略。方法如下:
的情形,我们就需要采用分治策略。方法如下:
- 分治:将棋盘尽可能平均的分割成4块;
- 合并:将4个子棋盘拼接。如下图:
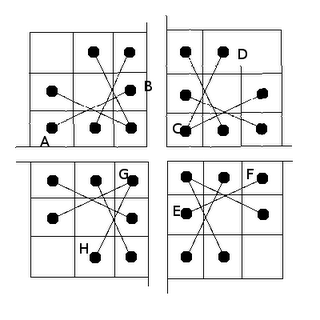
这时,为了合并4个子棋盘,对于原有的边A-B、C-D、E-F、G-H,我们将它们变为A-G、B-D、C-F、E-H,这样就合并了4个子棋盘。至此,分治的过程结束。
上面的解法只是求得一个Hamilton回路,但是对于条件更弱的Hamilton通路,我们并没有类似的算法。
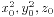 是方程x2+y2=z2的一个本原解,所以x0和y0必然是一奇一偶,不妨设2|y0,以及(y0,z0)=1。
是方程x2+y2=z2的一个本原解,所以x0和y0必然是一奇一偶,不妨设2|y0,以及(y0,z0)=1。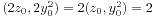 ,由此及2不整除
,由此及2不整除 即得
即得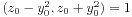 。我们又有
。我们又有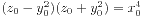
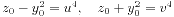 。这里v>u>0,(u,v)=1,u,v都是奇数。进而有
。这里v>u>0,(u,v)=1,u,v都是奇数。进而有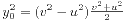
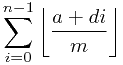
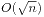 和
和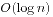 两种算法。
两种算法。
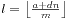 条。那么,我们对每条直线进行观察,发现如果我们只是求一条直线上有多少交点,是可以在O(1)的时间之内计算的。对于一条直线y=km,我们可以求出所有的交点数是
条。那么,我们对每条直线进行观察,发现如果我们只是求一条直线上有多少交点,是可以在O(1)的时间之内计算的。对于一条直线y=km,我们可以求出所有的交点数是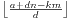 。
。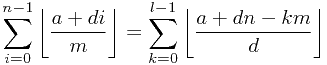
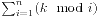 。
。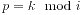 ,
,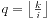 。那么当i增大1时,如果q不变,p一定减少了q,那么将p一直减小到0,同时对这一段进行求和(用数列求和公式),同时i增大到下一段的开头。
。那么当i增大1时,如果q不变,p一定减少了q,那么将p一直减小到0,同时对这一段进行求和(用数列求和公式),同时i增大到下一段的开头。