三次方程就是形如ax3+bx2+cx+d=0的一类方程。如果a,b,c,d都是实数,那么我们确定至少有一个实数根。要确定根的实数或者复数的具体情况,要计算下列的判别式:
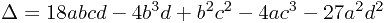
考虑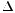 的正负情况:
的正负情况:
 ,那么只有一个实数解,另外两个解是复数解。
,那么只有一个实数解,另外两个解是复数解。 ,存在重根,但是所有解都是实数。
,存在重根,但是所有解都是实数。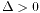 ,存在三个实数解。
,存在三个实数解。
另外,判别重根的问题可以参见我的另外一篇文章。
下面只是对三次方程的求解做一些简单的介绍。由于直接的求根公式可以从各种途径找到,在此不再重复。对于可以找到一个解的情况,我们可以因式分解来得到一个二次方程,而后解出其余两个解。
三次方程最早的解法是由波斯的数学家欧玛尔·海亚姆提出的,他采用了一种圆锥截面与圆相交的方法,至于具体情况我不是很清楚。南宋的秦九韶也对这个问题提出了自己的看法,提出了“正负开方术”,原则是“商常为正,实常为负,从常为正,益常为负”,并且可以扩充到任何高次方程中去。其实我们可以发现,秦九韶对高次方程非常有兴趣,他为了展示自己解方程的技巧,曾经构造出一个十次方程来,并命名为“开连枝某乘方”(“开玲珑某乘方”)。
后来到了16世纪,费罗找到了形如x2+mx=n方程的解法。其实如果允许复数存在,任何三次方程都是可以被化归为这个形式的。塔塔利亚很快也找到了一个方法,并且告诉了卡尔丹诺。卡尔丹诺以自己的名义发表了这个做法,据说塔塔利亚非常生气,并与之绝交。但是由于塔塔利亚的方法里面有时候需要对负数进行开方,所以也推动了复数理论的诞生。拉斐罗·邦别利很快就注意到了这些,并因此被人们认为是复数的发现者。
三次方程的求根公式一般而言有两种:一种是纯代数解,一种使用三角函数来表示。
我们先来看看卡尔丹诺的方法。首先我们可以很快将方程化为x3+bx2+cx+d=0的形式,只需要令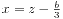 ,就可以消去二次项,从而得到z3+pz+q=0。我们令z=u+v,得到(u+v)3+p(u+v)+q=0,因式分解得到(u3+v3+q)+(u+v)(3uv+p)=0,由于u,v的值是不确定的,所以我们可以再加上一个条件3uv+p=0,这样我们得到u3+v3+q=0。至此,我们可以解出u和v,可以接下来得到三次方程的解。需要注意的是,在复数域中,求解u,v的时候要考虑三种情况。
,就可以消去二次项,从而得到z3+pz+q=0。我们令z=u+v,得到(u+v)3+p(u+v)+q=0,因式分解得到(u3+v3+q)+(u+v)(3uv+p)=0,由于u,v的值是不确定的,所以我们可以再加上一个条件3uv+p=0,这样我们得到u3+v3+q=0。至此,我们可以解出u和v,可以接下来得到三次方程的解。需要注意的是,在复数域中,求解u,v的时候要考虑三种情况。
我们也可以通过归纳法来求解方程。我们观察得到三次方程解得形式一定是![$x=\sqrt[3]{A}+\sqrt[3]{B}$ $x=\sqrt[3]{A}+\sqrt[3]{B}$](/user_files/rchardx/epics/9b0aea1c549332fea9d2eabf9d9fc2bc0a0b3225.png) 。那么我们得到
。那么我们得到![$x^3=(A+B)+3\sqrt[3]{AB}x$ $x^3=(A+B)+3\sqrt[3]{AB}x$](/user_files/rchardx/epics/9a99fd141a4ade454372640ec7d512aa9fc3f1d3.png) 。移项化简得到x3+px+q=0的形式,这里
。移项化简得到x3+px+q=0的形式,这里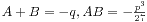 。所以可以化归为二次方程两个根的韦达定理。从而进一步就可以求出用p,q表示的x的解。这里A,B只是起到了一个中间变量的作用。
。所以可以化归为二次方程两个根的韦达定理。从而进一步就可以求出用p,q表示的x的解。这里A,B只是起到了一个中间变量的作用。
三次方程解的形式还是有很多的。对于x3+px+q=0形式的方程,我们还有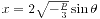 形式的解,其中
形式的解,其中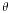 满足
满足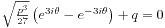 。但其实这也只是将变量x用
。但其实这也只是将变量x用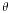 代换的结果。
代换的结果。
还有一些结论性的结果可以在Wikipedia上面找到,我想要说的大概就到这里了。
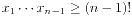 ,所以n>(n-1)!>(n-1)(n-2),解得
,所以n>(n-1)!>(n-1)(n-2),解得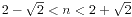 ,于是n=2或3。又x1+...+xn=x1...xn, 解得n=2时x1=x2=2,舍弃,所以n=3,易解得x1=1,x2=2,x3=3。 问题得解。
,于是n=2或3。又x1+...+xn=x1...xn, 解得n=2时x1=x2=2,舍弃,所以n=3,易解得x1=1,x2=2,x3=3。 问题得解。