Mar 20

SPOJ Problems Solved

Art of Science 0 Comments
  • 1 - Life, the Universe, and Everything[TEST]
    模拟题，只需要按照要求做就可以了。
  • 2 - Prime Generator[PRIME1]
    先用筛法求出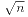$\sqrt{n}$范围内的质数，然后对指定的区间再使用筛法就可以了。不需要特别的优化。
  • 4 - Transform the Expression[ONP]
    中缀转后缀，经典问题，用栈操作就可以了。
  • 5 - The Next Palindrome[PALIN]
    只需要提取出前半部分，然后累加再判断是否符合要求就可以了。
  • 6 - Simple Arithmetics[ARITH]
    注意到水平线的长度只和直接相邻的上下两行有关。
  • 8 - Complete the Sequence![CMPLS]
    见SPOJ 8 - Complete the Sequence![CMPLS]。
  • 10 - Complicated Expressions[CMEXPR]
    利用中缀转后缀的结果进行去括号是比较稳妥的做法。分析表达式树也是可行的。
  • 11 - Factorial[FCTRL]
    简单题。
  • 14 - I-Keyboard[IKEYB]
    见SPOJ 14 - I-Keyboard[IKEYB]。
  • 15 - The Shortest Path[SHPATH]
    见SPOJ 15 - The Shortest Path[SHPATH]。
  • 16 - Sphere in a tetrahedron[TETRA]
    见SPOJ 16 - Sphere in a tetrahedron[TETRA]。
  • 22 - Triangle From Centroid[TRICENTR]
    平面几何题。我们先求出基本的三边长、三条高的长度。然后，建立坐标系，算出外心的坐标。由欧拉线的性质可知，重心到外心的距离是重心到垂心距离的一半，所以可以得到答案。
  • 23 - Pyramids[PIR]
    与TETRA一题方法一样。
  • 24 - Small factorials[FCTRL2]
    简单题。
  • 25 - Pouring water[POUR1]
    见SPOJ 25 - Pouring water[POUR1]。
  • 27 - Sorting Bank Accounts[SBANK]
    就是简单的排序，用gets()应该可以保证不会超时。
  • 29 - Hash it![HASHIT]
    Hash表的简单应用。
  • 31 - Fast Multiplication[MUL]
    高精度乘法，可以使用FFT等算法。其实直接压位也可以过。
  • 32 - A Needle in the Haystack[NHAY]
    KMP算法就可以过了。不过如果按照题目中给的提示，采用动态内存分配程序似乎有点慢。
  • 33 - Trip[TRIP]
    动态规划，没什么难度。
  • 39 - Piggy-Bank[PIGBANK]
    背包问题，动态规划解决之。
  • 40 - Lifting the Stone[STONE]
    求多边形的重心，一般采用三角剖分做，剖分的中心点往往是原点。
  • 42 - Adding Reversed Numbers[ADDREV]
    简单题。
  • 54 - Julka[JULKA]
    简单题。
  • 375 - Query on a tree[QTREE]
    见SPOJ 375 - Query on a tree[QTREE]。
  • 861 - Counting inversions[SWAPS]
    见SPOJ 861 - Counting inversions[SWAPS]。
  • 1644 - Trees[TREEOI14]
    见SPOJ 1644 - Trees[TREEOI14]。
Mar 20

SPOJ 14 - I-Keyboard[IKEYB]

Art of Science 0 Comments

动态规划。我们先预处理出必要的区间段信息，然后发现其满足单调性，于是采用单调性优化。我们使用的是f(x)=min{f(i)+w(i,x)}这一经典模型，二分求出决策就可以了，总的复杂度是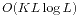$O(KL\log L)$。

#include <cstdio>
#include <climits>
#include <cstring>
#include <stack>

using namespace std;

const int MAXN = 90+5;

struct status {
  int u,b,e;
  status(int _u,int _b,int _e)
    : u(_u),b(_b),e(_e) {}
  status() {}
};

char ma[MAXN],mb[MAXN];
int n,m,f[MAXN][MAXN],w[MAXN];
int p[MAXN][MAXN],r[MAXN],g[MAXN][MAXN];
stack<status> st[MAXN];
int tdec[MAXN];

int main() {
  int ncase;
  scanf("%d",&ncase);
  for (int loop = 1; loop<=ncase; loop++) {
    scanf("%d%d",&m,&n);
    scanf("%s%s",ma,mb);
    for (int i = 1; i<=n; i++)
      scanf("%d",&w[i]);
    for (int i = 1; i<=n; i++) {
      g[i][i] = w[i];
      for (int j = i+1; j<=n; j++)
        g[i][j] = g[i][j-1]+w[j]*(j-i+1);
    }
    f[0][0] = 0;
    st[1].push(status(1,1,n));
    for (int i = 1; i<=m; i++) {
      while (!st[i].empty()) {
        status tmp = st[i].top();
        for (int j = tmp.b; j<=tmp.e; j++)
          p[i][j] = tmp.u;
        st[i].pop();
      }
      for (int j = i; j<=n; j++)
        f[i][j] = f[i-1][p[i][j]-1]+g[p[i][j]][j];
      if (i<m) {
        st[i+1].push(status(i+1,i+1,n));
        for (int j = i+2; j<=n; j++) {
          while (!st[i+1].empty()) {
            int u = st[i+1].top().u;
            int b = st[i+1].top().b;
            if (j<=b && f[i][u-1]+g[u][b]>f[i][j-1]+g[j][b])
              st[i+1].pop();
            else break;
          }
          int u = st[i+1].top().u;
          int e = st[i+1].top().e;
          if (j<=e && f[i][u-1]+g[u][e]>f[i][j-1]+g[j][e]) {
            int l = st[i+1].top().b,r = e; // (]
            while (l+1<r) {
              int mid = (l+r)/2;
              if (j<=mid && f[i][u-1]+g[u][mid]>f[i][j-1]+g[j][mid]) r = mid;
              else l = mid;
            }
            st[i+1].top().e = l;
            st[i+1].push(status(j,l+1,n));
          }
          else if (e+1<=n) st[i+1].push(status(j,e+1,n));
        }
      }
    }
    for (int i = m,j = n; i>0; i--) {
      r[i] = p[i][j];
      j = r[i]-1;
    }
    r[m+1] = n+1;
    printf("Keypad #%d:\n",loop);
    for (int i = 1; i<=m; i++) {
      printf("%c: ",ma[i-1]);
      for (int j = r[i]; j<r[i+1]; j++)
        printf("%c",mb[j-1]);
      printf("\n");
    }
    printf("\n");
  }
  return 0;
}

Your program in C++ from 2010-03-19 08:54:48 ran for 0.53 seconds and used 2792 KB of memory.

Mar 19

SPOJ 8 - Complete the Sequence![CMPLS]

Art of Science 3 Comments

题目给出了一个数列的前若干项，要求推测后面的项。我们很容易想到拉格朗日插值法，但是精度就变成了一个大问题。这个问题虽然保证了所有的值都是整数，但是并没有保证其多项式的系数也是整数，因此在计算方面存在很大的困难。

除了插值法，求解这种数列问题我们有更好的差分方法，过程中完全不涉及浮点数操作。比如说，对于1 2 4 7 11 16 22 29这个数列，我们对于每一项做其和前一项的差，也就是2-1=1, 4-2=2, 7-4=3, ....这样，我们得到一个1阶差分：1, 2, 3, 4, 5, 6, 7。我们再求得2阶差分是：1, 1, 1, 1, 1, 1。这时，规律已经有些明显了。

也就是说，对于任意一个存在合理多项式通项的数列，用差分的方法是可以得到它的解的：只要求得这个n项数列的n-1阶差分，然后倒推回去就可以了。代码如下：

#include <cstdio>
#include <cstring>

using namespace std;

const int MAXN = 100+5;

int n,m,s[MAXN][MAXN];

int main() {
  int ncase;
  scanf("%d",&ncase);
  while (ncase--) {
    scanf("%d%d",&n,&m);
    for (int i = 0; i<n; i++)
      scanf("%d",&s[0][i]);
    for (int i = 1; i<n; i++)
      for (int j = 0; i+j<n; j++)
        s[i][j] = s[i-1][j+1]-s[i-1][j];
    for (int i = 1; i<=m; i++)
      s[n-1][i] = s[n-1][0];
    for (int i = n-2; i>=0; i--)
      for (int j = 0; j<m; j++)
        s[i][n-i+j] = s[i][n-i+j-1]+s[i+1][n-i+j-1];
    for (int i = 0; i<m-1; i++)
      printf("%d ",s[0][n+i]);
    printf("%d\n",s[0][n+m-1]);
  }
  return 0;
}

Your program in C++ from 2010-03-18 12:22:31 ran for 0.52 seconds and used 2576 KB of memory.

Feb 24

戴德金分割理论（Dedekind Cut）

Art of Science 1 Comments

对于实数集这个概念，我们有一些很好的基本性质：

  • 实数集是一个有序集；
  • 实数集是稠密的；
  • 实数集中四则运算具有封闭性。

当然，这些性质并不能严格地给出实数的定义，戴德金分割理论正是为此而产生的一个理论。

戴德金理论是一种对集合进行划分的方法。前提是这个集合是可以严格排序的。方法把待分割的集合分成两个交集为空且自身不为空的集合A和B，而且A中的任何元素都比B中的元素小。我们令全集为U，那么形式化的：

  • $A\cup B=U$；
  • $A\cap B=\phi$，$A,B\neq \phi$；
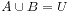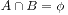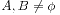  • 对于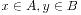$x\in A,y\in B$，必然有x<y。

显然，对于A和B中最大值和最小值的情况有四种情况。

首先，整数集、有理数集、实数集都是存在戴德金分割的。对于整数集来说，由于不存在稠密性，分割中A必定存在最大值，B必定存在最小值。我们可以把相应的最值称为边界数。而对于有理数集和实数集而言，要么A中存在最大值，要么B中存在最小值，必定满足且仅满足其中的一个。这很容易证明，如果同时满足，那么根据有理数集和实数集的稠密性，两个边界数中必定还存在一个既不属于A又不属于B的数，与分割的定义矛盾。

所以我们可以根据有理数集的戴德金分割来定义实数集。

对于有理数集Q的一个戴德金分割，如果A中存在最大值或者B中存在最小值，那么就定义了一个有理数；如果A中没有最大值，B中也没有最小值，那么就定义了一个无理数。实际上，分割的情况不外乎下面三种：

  • $A=\{x<r\},B=\{x\geq r\}$；
  • $A=\{x\leq r\},B=\{x>r\}$；
  • $A=\{x<r\},B=\{x>r\}$。

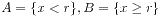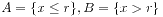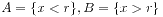前面两种情况就定义了有理数r，最后一种情况则定义了无理数r。之所以会有这种区别，是因为实数集具有连续性。

如果我们规定有理数集的戴德金分割不允许集合A有边界数，那么可以建立分割和实数的一一对应关系，在有理数的基础上定义了实数，这为数学分析奠定了基础。

Feb 22

最小树形图

Art of Science 1 Comments

最小树形图就是最小生成树在带权有向图上面的变种，也就是在有向图上找出一个边权和最小的有向树。这个问题需要给定一个带权的有向图以及有向树的根节点v。所谓有向树是指除了叶节点以外，所有节点都有指向其孩子节点的有向边。专业一点的说，“有向树（Directed Tree）是一个用于定义数据流或流程的逻辑结构。数据流的源点是根。数据流是单向分支离开根部到达目标，这个目标就是有向树的叶子。”。

求解最小树形图的第一个算法是1965年朱永津和刘振宏提出的复杂度为O(VE)的算法，该算法被称为朱-刘算法。在实现过程中，我们也可以表达为O(V3)的复杂度。

首先我们需要判断解是否存在。为了解决这个问题，我们只需要从指定的根节点v除法遍历一次就可以了。如果所有节点都可以被访问，那么解显然存在，否则不存在。另外，图中所有的自环也必须清除，因为这些自环显然不可能是最小树形图中的边。如果不知道什么是自环，请自行查阅图论相关定义。消除自环的目的是保证算法的时间复杂度。

下面是算法的流程：

  1. 对于图中除了根节点v以外的节点，选择一条权值最小的入边。所有被选择的边构成了一个子图，如果这个子图不含有有向环，那么这就是问题的解，算法结束；否则进行下一步。
  2. 我们需要收缩有向环，并且用一个新节点来代替。对于环中的点x，假定其选择边的权值为w0，y为环外的点，z为环收缩后新的节点。如果存在边<x,y>，那么<z,y>的边权值与<x,y>相同。如果存在边<y,x>且权值为w，那么新边<y,z>的权值就是w-w0。
  3. 重复执行1、2两个步骤。

要保证算法O(VE)的复杂度，要做到找最小入边O(E)，找环O(V)，收缩O(E)。再加上由于收缩环最多只进行V-1次（自环已经被消除），所以时间复杂度为O(VE)。在步骤2中，x的出边权值不变是因为收缩环并没有影响边所指向的节点，而入边的权值之所以要变小，是因为当新边被选择之后，x原来选择的入边就会被取消选择，所以实际花费的代价就是w-w0。

以下是2道可以提交的题目。

  • [UVa]11183 - Teen Girl Squad
  • [PKU]3164 - Command Network