题目描述在这里。
题目的意思就是给定一个正整数n(n不超过9*1014),要求我们给出有多少种方式,使得n能够表示为若干个连续正整数的和。比如n=9,那么有3种方式:2+3+4,4+5,9。
我们可以假定a+(a+1)+...+(b-1)+b=n,也就是(b+a)*(b-a+1)=2n。而(b+a)+(b-a+1)=2b+1是一个奇数,说明(b+a)和(b-a+1)具有不同的奇偶性,必然有一个是奇数。我们先把n当中所有素因数2从等式两边约去,同时考虑到(b+a)和(b-a+1)奇偶性不同,就可以把问题转化为n的奇数约数有多少个。由于这里的a和b是不受n的限制的变量,我们只要得到一个奇数约数必然可以求出相应的a和b(注意到(b+a)-(b-a+1)=2a-1是一个正整数,所以(b+a)>(b-a+1)。)。比如n=12,给出一个奇数约数3,那么a=3,b=5;给出一个奇数约数1,那么a=b=12。
现在我们所要做的就是对n进行质因数分解,然后用各个素因数的指数求解。显然,O(n1/2)的算法是不够的。我们要具体考察一下素因数分解的过程。如果用[2,L]以内的素数进行分解,那么约去所有因数后,最后剩下的n'一定不含有该范围的任何质数,也就是说n'如果小于L2,那么一定是素数;如果大于L2,那么只需要判断n'到底是不是素数。我们注意到,如果n'不是素数且只含有两个素因数,我们是可以分析出结果的,也就是说,我们需要排除n'含有三个素因数的情况。注意到(105)3略大于9*1014,我们就找到了方法。
先预处理出[2,105]范围内所有的素数,并且对n进行分解。然后按照上面的方法对分解的结果n'进行讨论,关于判断n'是否是素数,我们可以用Miller-Rabin素性测试来解决,Java中可以借助BigInteger的isProbablePrime来判断。整个算法的复杂度约为O(n1/3),下面就是代码,UVa上面的提交结果是运行了0.556s:
import java.math.*;
import java.util.*;
class Main {
private final static int MAXP = 100000;
private final static long LIMIT = (long)MAXP*MAXP;
private static int[] primes;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
getprimes();
while (in.hasNextLong()) {
long n = in.nextLong();
System.out.println(solve(n));
}
}
private static int solve(long n) {
if (n==0) return 0;
while ((n&1)==0) n >>= 1;
int ans = 1;
for (int i = 0; i<primes.length; i++) {
long t = primes[i];
if (t*t>n) break;
int cnt = 0;
while (n%primes[i]==0) {
n /= primes[i];
cnt++;
}
ans *= cnt+1;
}
if (n==1);
else if (n<LIMIT || BigInteger.valueOf(n).isProbablePrime(16))
ans *= 2;
else {
long tmp = (long)(Math.sqrt(n)+1e-6);
if (tmp*tmp==n) ans *= 3;
else ans *= 4;
}
return ans;
}
private static void getprimes() {
boolean[] isp = new boolean[MAXP+1];
int size = 0,ptr = 0;
for (int i = 2; i<=MAXP; i++)
if (!isp[i]) {
size++;
for (int j = 2*i; j<=MAXP; j += i)
isp[j] = true;
}
primes = new int[size];
for (int i = 2; i<=MAXP; i++)
if (!isp[i]) primes[ptr++] = i;
}
}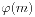 。我们可以联想其形式:
。我们可以联想其形式: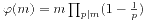 。那么当n>1时我们也来类比一下相对应的公式。
。那么当n>1时我们也来类比一下相对应的公式。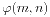 表示题目中所要求的答案。我们发现,当m为素数时,
表示题目中所要求的答案。我们发现,当m为素数时, 。这是显然的,因为除了(m,m,...,m,m)这一组数字以外,其余的都是可行的解。那么m不为素数时,我们把m的各个素因数分开考虑。如果某个素因数被n个数所共有,那么一共就少了
。这是显然的,因为除了(m,m,...,m,m)这一组数字以外,其余的都是可行的解。那么m不为素数时,我们把m的各个素因数分开考虑。如果某个素因数被n个数所共有,那么一共就少了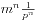 种方案,考察m所有的素因数,我们得到
种方案,考察m所有的素因数,我们得到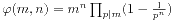 。
。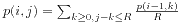 ,边界条件是i=0时p(i,j)=1。如果一个询问的两点之间长度为d,预算为b,直接输出p(d,b)就可以了。
,边界条件是i=0时p(i,j)=1。如果一个询问的两点之间长度为d,预算为b,直接输出p(d,b)就可以了。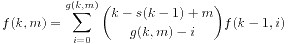
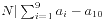 。那么所有序列的
。那么所有序列的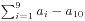 的最大公约数在有解的情况下就是问题的答案。
的最大公约数在有解的情况下就是问题的答案。