richard-desktop

(*O/*_/
Cu  #%* )pop mark/CuG 4 def/# 2 def%%%%@@P[TX---P\P_SXPY!Ex(mx2ex("SX!Ex4P)Ex=
CuG #%*                                                                  *+Ex=
CuG #%*------------------------------------------------------------------*+Ex=
CuG #%*   POLYGLOT - a program in seven languages      15 February 1991  *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*   Written by Kevin Bungard, Peter Lisle, and Chris Tham          *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*   We have successfully run this program using the following:     *+Ex=
CuG #%*     ANSI COBOL:            MicroFocus COBOL85 (not COBOL74)      *+Ex=
CuG #%*     ISO  Pascal:           Turbo Pascal (DOS & Mac), Unix PC,    *+Ex=
CuG #%*                            AIX VS Pascal                         *+Ex=
CuG #%*     ANSI Fortran:          Unix f77, AIX VS Fortran              *+Ex=
CuG #%*     ANSI C (lint free):    Microsoft C, Unix CC, GCC, Turbo C++, *+Ex=
CuG #%*                            Think C (Mac)                         *+Ex=
CuG #%*     PostScript:            GoScript, HP/Adobe cartridge,         *+Ex=
CuG #%*                            Apple LaserWriter                     *+Ex=
CuG #%*     Shell script:          gnu bash, sh (SysV, BSD, MKS), ksh    *+Ex=
CuG #%*     8086 machine language: MS-DOS 2.00, 3.03, 4.01, 5.00 beta    *+Ex=
CuG #%*                            VPix & DOS Merge (under unix)         *+Ex=
CuG #%*                            SoftPC (on a Mac), MKS shell          *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*   Usage:                                                         *+Ex=
CuG #%*     1. Rename this file to polyglot.[cob|pas|f77|c|ps|sh|com]    *+Ex=
CuG #%*     2. Compile and/or run with appropriate compiler and          *+Ex=
CuG #%*        operating system                                          *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*   Notes:                                                         *+Ex=
CuG #%*     1. We have attempted to use only standard language features. *+Ex=
CuG #%*        Without the -traditional flag gcc will issue a warning.   *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*     2. This text is a comment block in all seven languages.      *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*     3. When run as a .COM file with MS-DOS it makes certain      *+Ex=
CuG #%*        (not unreasonable) assumptions about the contents of      *+Ex=
CuG #%*        the registers.                                            *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*     4. When transfering From Unix to DOS make sure that a LF     *+Ex=
CuG #%*        is correctly translated into a CR/LF.                     *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*   Please mail any comments, corrections or additions to          *+Ex=
CuG #%*   peril@extro.ucc.su.oz.au                                       *+Ex=
CuG #%*                                                                  *+Ex=
CuG #%*------------------------------------------------------------------*QuZ=
CuG #%*                                                                  *+Ex=
CuG #%*!Mx)ExQX4ZPZ4SP5n#5X!)Ex+ExPQXH,B+ExP[-9Z-9Z)GA(W@'UTTER_XYZZY'CPK*+
CuG #(*                                                                  *(
C   # */);                                                              /*(
C   # *)  program        polyglot (output);                             (*+
C   #     identification division.
C   #     program-id.    polyglot.
C   #
C   #     data           division.
C   #     procedure      division.
C   #
C   # * ))cleartomark   /Bookman-Demi findfont 36 scalefont setfont     (
C   # *                                                                 (
C   #
C   # *                  hello polyglots$
C   #     main.
C   #         perform
C     * ) 2>_$$; echo   "hello polyglots"; rm _$$; exit
print
C             stop run.
-*,                'hello polyglots'
C
C         print.
C             display   "hello polyglots".                              (
C     */  int i;                                                        /*
C     */  main () {                                                     /*
C     */      i=printf ("hello polyglots\n"); O= &i; return *O;         /*
C     *)                                                                (*
C     *)  begin                                                         (*
C     *)      writeln  ('hello polyglots');                             (*
C     *)                                                                (* )
C     * ) pop 60 360                                                    (
C     * ) pop moveto    (hello polyglots) show                          (
C     * ) pop showpage                                                  ((
C     *)
end                                                          .(* )
C)pop%     program       polyglot.                                      *){*/}

这个工具叫做msf-abbrev，这里是它的主页。

照着里面的说明配置就可以了，这里放出我自己的配置： 

(add-to-list 'load-path "~/emacs")
(setq-default abbrev-mode t)
(setq save-abbrevs nil)

(require 'cc-mode)

(require 'msf-abbrev)
(setq msf-abbrev-verbose t)
(setq msf-abbrev-root "~/emacs/mode-abbrevs")
(global-set-key (kbd "C-c l") 'msf-abbrev-goto-root)
(global-set-key (kbd "C-c a") 'msf-abbrev-define-new-abbrev-this-mode)
(msf-abbrev-load)

这样就可以用C-c a来添加新的缩写。

在主页上可以下载到demo，这里是地址。如何编写自己的abbrev，可以参考里面的文件，语法很简单。

最短增广路，顾名思义，就是一条增广路，而且还是所有增广路中最短的一条。要求出最短增广路也十分容易，只要在残量网络中求出源点到汇点的最短路就可以了（所有边的长度为1）。

求出了最短增广路，我们就可以沿着它对网络进行增广，而且可以证明，如果只要求最大流，最多经过n（n为总结点数）次增广，就可以求出最大流。实现也非常简单，由于所有边的长度为1，所以只需要使用宽搜。使用最短增广路的方法求最大流，其实也是Ford-Fulkerson方法的一种，这种方法的特点是每次找出一条残量网络中的增广路径并进行增广。整个过程中满足流的网络的三个性质：容量限制、反对称性、流守恒性。

如果不知道什么是残量网络（或者又被叫做残留网络），请看下面的解释。

• 残量：容量－流量。
• 残留边：有残留容量的边成为残留边
•  残留网络：由网络的点集、残留边集构成残留网络。

这里我们需要注意一点，宽搜的结果如果可以为后面所利用的话，我们就可以写出一种新的求最大流的算法：SAP，全称Shortest Augmenting Path Algorithm。其时间复杂度为O(n²m)。在实践中，这种算法效率还是比较高的，而且性价比相当好（我一般都会使用它）。

在SAP中，定义每个点的距离标号，即残留网络中点到汇点的距离。然后，只需要在距离标号相邻的点间寻找增广路径。如果从一个点出发没有可行边，就对该点进行重标记，然后并回溯（类似预流推进算法）。

可行边就是说，存在一条边<i,j>，当且仅当r_i,j>0且d_i=d_j+1时，边是容许边，我们的算法只考虑容许边（这里d指距离标号，r指残量网络中的流量）。

算法的一开始，我们从汇点t进行一次宽搜求出距离标号（或者也可以不进行预处理，直接赋值为0，因为随着重标记的过程，距离标号会自行调整），然后从源点s开始递归操作（或者也可以不递归，因为算法本身并不繁琐）。对于一个点i，如果存在容许边<i,j>，当j是汇点时增广并从源点开始递归，否则就令i是j的前驱，并递归j。否则对i重标号，使得d_i=min{d_j|r_i,j>0}+1，并回溯。当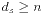时算法停止，此时不存在任何一条增广路。

当然我们可以参考预流推进，对它进行间隙优化。同时还有一个叫做当前弧的优化，采用后速度也有一定的提升。而且，采用前向星的储存方式会更好。

我们也可以用最短增广路来求最小费用最大流，原理不需要再阐述了，如果是用增广路算法来求最小费用最大流，就是要找一条费用最少的路径来进行增广。当然可以套用最短增广路的方法来做。 

问题概述：有n个女生和n个男生，每位女生按照她的偏爱程度将男生排序，同时每位男生也按照自己的偏爱程度将女生排序，然后将这n个女生和n个男生配成完备婚姻。

如果存在两位女生A和B，两位男生a和b，使得A和a结婚，B和b结婚，但是A更偏爱b而不是a，b更偏爱A而不是B，则这 个婚姻就是不稳定的。反之，这个婚姻就是稳定的。

可以通过证明，得到每一个n女n男的社团，都存在稳定婚姻的结论。但是这种情况只在异性的社团中存在。也就是说在同性的社团里面，稳定婚姻的存在性将不再被保证。下面是一种简单的稳定婚姻的算法。

Gale-Shapley 算法： 

while存在男人m是自由的且还没对每个女人都求过婚
   选择这个男人m
   令w是m的优先表中还没求过婚的最高排名的女人
   if w 是自由的
       (m,w)变成约会状态
   else
       w当前与m1约会
       if w更偏爱m1而不爱m
           m保持自由
       else
           w更偏爱m而不爱m1
           (m,w)变成约会状态
           m1变成自由
       endif
   endif
endwhile

一道关于稳定婚姻问题的题目：ZJU 1576 Marriage is Stable。

 二分图最大权完美匹配KM算法是在一个二分图里，求一个最大权匹配，但是要求这个匹配必须是完美匹配。如果匹配不一定是完美匹配，那么似乎只能将其转化为最小费用最大流来做了。我们可以使用KM算法对任意带权（无论正负权）二分图求最大/最小权完美匹配，它的算法复杂度是O(n³)，但是如果写得不好会变成O(n⁴)。

KM算法是通过给每个顶点一个标号（我们有时称之为顶标）来把求最大权匹配的问题转化为求完备匹配的问题的。我们令二分图中X部的节点的顶标为A_i，Y部的节点的顶标为B_i。X部与Y部节点之间的权值为W_i,j，那么，在算法进行的过程中，我们必须始终保持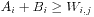成立。因为KM算法的正确性基于以下定理：

若由二分图中所有满足A_i+B_i=W_i,j的边 (i,j)构成的子图（称做相等子图）有完备匹配，那么这个完备匹配就是二分图的最大权匹配。

初始时为了使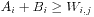成立，令A_i为所有与X_i顶点关联的边的权值的最大值，令B_i=0。如果当前的相等子图没有完备匹配，就需要修改顶标以使扩大相等子图，直到相等子图具有完备匹配为止（这样就可以求出最大权匹配）。

如果当前相等子图找不到完备匹配，那么是因为对于某个X顶点，我们找不到一条从它出发的交错路。这时我们获得了一棵交错树，现在我们把交错树中X部的顶点的顶标全都减小某个值d，Y部的顶点的顶标全都增加d，就可以使得至少有一条新边进入相等子图。这里d=min{A_i+B_i-W_i,j}，而且X_i在交错树中，Y_i不在。

但是如果仅仅是这样，用朴素的方法实现，算法复杂度是O(n⁴)。我们给每个Y部的顶点一个“松弛量”slack，每次开始找增广路时松弛量初始化为无穷大。在寻找增广路的过程中，检查边(i,j)时，如果它不在相等子图中，则让slack_j变成原值与A_i+B_i-W_i,j的较小值。这样，在修改顶标时，取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。但还要注意一点：修改顶标后，要把所有的slack_j值都减去d。经过这样一个优化实现后，算法复杂度就变成了O(n³)。