Jan 11

介绍四种GCC内置位运算函数

Code and Develop 0 Comments
  • int __builtin_ffs (unsigned int x)
    返回x的最后一位1的是从后向前第几位，比如7368（1110011001000）返回4。
  • int __builtin_clz (unsigned int x)
    返回前导的0的个数。
  • int __builtin_ctz (unsigned int x)
    返回后面的0个个数，和__builtin_clz相对。
  • int __builtin_popcount (unsigned int x)
    返回二进制表示中1的个数。
  • int __builtin_parity (unsigned int x)
    返回x的奇偶校验位，也就是x的1的个数模2的结果。

此外，这些函数都有相应的usigned long和usigned long long版本，只需要在函数名后面加上l或ll就可以了，比如int __builtin_clzll。

Jan 11

求正整数集合使得元素之和等于元素之积

Art of Science 0 Comments

这是一个比较有意思的正整数性质的应用。我们应该可以迅速找到一个解{1,2,3}，但是如果要说明这个解的唯一性，我们需要做出一些讨论。

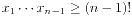令这个集合为S={x1,...,xn}，这里n>1，0<x1<...<xn。 我们得到nx1<x1...xn<nxn，于是x1...xn-1<n，而$x_1\cdots x_{n-1}\geq (n-1)!$，所以n>(n-1)!>(n-1)(n-2)，解得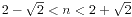$2-\sqrt{2}<n<2+\sqrt{2}$，于是n=2或3。又x1+...+xn=x1...xn， 解得n=2时x1=x2=2，舍弃，所以n=3，易解得x1=1,x2=2,x3=3。 问题得解。

Jan 11

Hello World!

Spirit and Thinking 0 Comments

我很久不写东西了，也就是说已经颓废了很久了。自从去年暑假之后，我的学习生活好像出现了一个断层。我突然对很多东西开始了不适应，对很多东西都厌烦了。 高三上学期的几次考试都是一落千丈。我自问不是一个特别喜欢浪费时间的人，但是在这样一个压抑的心理作用下，有时候颓废就会变成一种生活的方式。

但是，作为我内心来讲，生活不仅仅是有很多用来颓废的时间，还要很多东西我没有经历过。这篇日志算是我从这一刻开始不再颓废的证据，以后还是要好好利用自己 能够把握的时间，因为对于我来说，时间其实并不是很充裕。高三的放纵让我明白了一些东西，有时候我在想这是不是我有意而为。

总而言之，在接下来的 时间里面，好好把握每一分钟吧。