三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一
金一十大女支三金一十大女支三金一十大女支三金一十大女支三金一十大女支三三支女大十一
三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一
金一十大女支三金一十大女支三金一十大女支三金一十大女支三金一十大女支三三支女大十一
三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一
金一十大女支三金一十大女支三金一十大女支三金一十大女支三金一十大女支三三支女大十一
三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一
金一十大女支三金一十大女支三金一十大女支三金一十大女支三金一十大女支三三支女大十一
三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一
金一十大女支三金一十大女支三金一十大女支三金一十大女支三金一十大女支三三支女大十一
三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一金三支女大十一
金一十大女支三金一十大女支三金一十大女支三金一十大女支三金一十大女支三三支女大十一
偶然看到的,这些字确实给人一种扭曲的感觉。
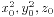 是方程x2+y2=z2的一个本原解,所以x0和y0必然是一奇一偶,不妨设2|y0,以及(y0,z0)=1。
是方程x2+y2=z2的一个本原解,所以x0和y0必然是一奇一偶,不妨设2|y0,以及(y0,z0)=1。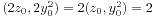 ,由此及2不整除
,由此及2不整除 即得
即得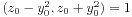 。我们又有
。我们又有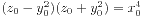
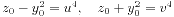 。这里v>u>0,(u,v)=1,u,v都是奇数。进而有
。这里v>u>0,(u,v)=1,u,v都是奇数。进而有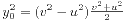
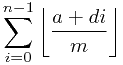
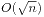 和
和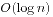 两种算法。
两种算法。
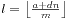 条。那么,我们对每条直线进行观察,发现如果我们只是求一条直线上有多少交点,是可以在O(1)的时间之内计算的。对于一条直线y=km,我们可以求出所有的交点数是
条。那么,我们对每条直线进行观察,发现如果我们只是求一条直线上有多少交点,是可以在O(1)的时间之内计算的。对于一条直线y=km,我们可以求出所有的交点数是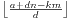 。
。