richard-desktop

完整的题目描述在这里。

题目给了我们一些货物的价格a₁,...,a_m（不超过100000），要我们构造一种货币面值的方案x₁,...,x_n，使得所需要的纸币数量尽可能少。货币面值的方案必须满足

• x₁=1。
• 对于i<j，x_i一定是x_j的约数。

注意到不需要给出面值的方案，只是要求输出最少的张数，那么我们可以用动态规划解决。对于一个确定的方案，由于上述的性质，我们一定是用贪心的方法来付款。另外，价格不会超过100000，所以需要考虑的最大面值也是100000。对于一个面额x_i，付完款之后得到的余额是a₁%x_i,...,a_m%x_i。我们令f(i)表示用面值大于等于i的货币方案所付款所需要的纸币数量， 那么f(i)=min{f(j)+余额用i付款的张数 | i为j的约数}。具体的代码如下：

public class NewCoins {
  static final int MAXN = 100000;
  public int minCoins(int[] price) {
    int n = price.length;
    int[] f = new int[MAXN+1];
    for (int i = MAXN; i>0; i--) {
      for (int j = 0; j<n; j++)
        f[i] += price[j]/i;
      for (int j = 2*i; j<=MAXN; j += i) {
        int tmp = f[j];
        for (int k = 0; k<n; k++)
          tmp += (price[k]%j)/i;
        if (f[i]>tmp) f[i] = tmp;
      }
    }
    return f[1];
  }
}

至此，问题就解决了。

C++果然是非常微妙的语言，%f和%lf对于printf()和scanf()的效果是不同的。

事实上，对于printf()，无论是%f还是%lf，效果都是一样的。因为，遇到float，printf()会将float类型自动提升到double，所以不会有什么问题。而且严格地讲，printf()并没有对于%lf的定义，虽然很多编译器会接受，所以最好使用%f。

而对于scanf()，由于接受的是指针，并没有类型提升的说法，所以对于double就应该用%lf，float就是%f。

SWERC2008主页在这里：SWERC 2008 - Nuremberg。这套题目还是一贯的欧洲赛区的风格，题目大多数都可以做。

• Bring Your Own Horse：题目很长很烦，从最后的Scoreboard就可以看出来很多人因为题目描述的原因没有看出来题目的意思。题目的要求很简单，就是先求一个最小生成树，然后对于每一个询问，都用一次BFS来找到生成树中两点之间路径当中最长的边。代码量并不大，但是最快的提交也用了66分钟，完全是题目描述的问题。
• First Knight：一个非常明显的高斯消元法，如果在中国赛区应该算是容易的。
• Postal Charges：一个别出心裁的降低复杂度的题目。巧妙的用类似桶排序的方法先进行分类，然后考虑到只是进行曼哈顿距离的计算，所以可以分块求解。每一个块中不同的元素都已经预处理出到自身所在块的左下角的距离，使用乘法原理就可以解决。
  

  double calc() {
    double sum = 0.0; //总长度
    int co = 0;       //路线数量
    for (int i = 1; i<MAX; i++)
      for (int j = 1; j<MAX; j++) //i,j枚举当前的块
        for (int k = 0; k<i; k++)
          for (int l = 0; l<j; l++) { //k,l枚举当前快之前的块
            //l[i][j]表示(i,j)这个块里面所有点的该块左下角的距离之和
            //c[i][j]表示每个块中含有元素的个数
            sum += l[i][j]*c[k][l]-l[k][l]*c[i][j]+(i-k+j-l)*c[i][j]*c[k][l]; //乘法原理
            co += c[i][j]*c[k][l]; //求和
          }
    return sum/co;
  }

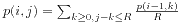• Randomly-priced Tickets：题目给定了一个无向图。首先用Floyd求出两点之间的距离，然后就是要求在一条定长的路线上分配初始的预算。这个问题用动态规划很容易解决。设p(i,j)表示长度为i的路线，预算为j，能够通过的可能性，那么，边界条件是i=0时p(i,j)=1。如果一个询问的两点之间长度为d，预算为b，直接输出p(d,b)就可以了。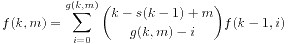
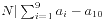• The Game：博弈问题，用最大最小搜索，Alpha-Beta剪枝应该会有好的效果。
• The Merchant Guild：动态规划。首先要确定方案合法的充要条件，就是最多不超过i个商人被分配到了最后的n-i+1个位置。这样令f(k,m)为在k,...,n之间还有m个空位时的分配方案数，s(k)表示前k个位置一共有多少本地商人，g(k,m)=m+1-s(k-1)+s(k-2)，那么
  
• Toll Road：分治。题目所给的是一个树，只要DFS一次，找出最大权值的子树就可以了，用分治法会很轻松。
• Top Secret：矩阵乘法。我们依据题意构造出矩阵之后进行计算，由于这是一个循环矩阵，可以把O(n³)的算法优化至O(n²)。
• Transcribed Books：数论题。注意到对于所有的序列，。那么所有序列的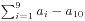的最大公约数在有解的情况下就是问题的答案。
• Wizards：数学题。详细情况请参见判断方程是否有重根。

还是接着上一篇《世界中的世界》来继续乱扯。说到底上一篇是讲了系统与系统内事物的关系，这是一种具有相对性的关系。我只是简单的阐述了一下我关于“封闭性”的想法，其实并没有什么实际或者理论上的根据。至于哲学方面我还是比较认同辩证唯物论的，这些想法基本上还是建立在其基础之上。

说到偶然，就会想起掷骰子，骰子每次向上的点数都是随机的，但是经过一定次数之后，每种点数的出现频率逐渐稳定。这就是一个简单的偶然转化为必然的例子。也就是虽然某一种个体具有一定不确定性，但是如果这些个体的集合足够多，还是能够预测出大概的情况。有人说，“你永远也不知道一个人下一刻会干什么，但是你能预测人类未来的走向。”，说的就是这个意思。

有这样一个数列1-1+1-1+1...，我们没有办法对其进行求和。它的数列项数虽然已经达到的充分多的要求（无限多），但是反而不能够进行求值。如果这是一个有限项数的数列，它的值反而能够求出，是不是有点匪夷所思。罗素说，历史是由一个个偶然的因素所构成的。比如，希特勒如果当初饿死在奥地利街头，会不会有后来的二次大战？我不赞成如今有些人无论关于什么事件都说是什么历史的必然，那历史岂不是很无趣？这些说法简直就是彻彻底底的宿命论。我不否认有些必然性的存在，但是一味强调必然而忽视偶然无疑是错误的。上面两个例子探讨了一下偶然和必然在数量上面的关系，我不得不承认这是我所不好回答的问题，或许这就是质变和量变的概念了。

但是偶然和必然关于个体的关系又是怎样的呢？倘若我们只研究一个个体？写到这里我又突然想到了“封闭性”，“封闭性”是从结果来分析过程，而这里却是要从过程来分析结果，岂不是很矛盾？唯一的解释就是这是基于两种不同的思想，所以我们暂时还没有解释的能力。我们暂且可以认为已经发生的事情是必然，那么正在发生的事情就是偶然，偶然之中产生了必然，这事怎样的一种关系？蝴蝶在太平洋上扇了一下翅膀，在大西洋上却引发了飓风。偶然之中有着必然，必然之中也有着偶然。瞬间的偶然却将形成既有的事实，那瞬间和永恒又是什么样的关系？必然又印证着瞬间的偶然，就像一幕幕的电影胶片，每一幕都定格了一次必然，但是你不会知道下一幕是什么。

我还是来自我总结一下吧。所谓偶然，就是我现在坐在电脑面前码字，但是我下一刻很有可能突发奇想想要跳楼，于是就从窗户跳下去了。虽然这种可能性非常之小，但是也是一种可能。有所谓的“分叉”的宇宙就是基于这个想法，不断的考虑各种分支情况而产生了一个复杂的宇宙集合。这种想法有一定道理，但是未必正确。发生了就是发生了，没发生的就是没发生，所以我这一辈子也不一定会跳楼。这是一种微妙的感觉，我明白自己有这种想法，但是我现在可以控制住它，也就是当前的系统环境不会给予它发生的可能。那么，偶然的存在是否就是因为运动的关系？事物都在不断的运动之中，环境也在不断变化，前一刻可以控制的，下一刻却无能为力。这样看起来，必然就是存在于运动的偶然之中，取决于瞬息之间环境的因素。

但是这好像又忽视了不可抗力的干扰。一切物体本身都是具有不确定性，如果这不确定性不是由运动影响的，那就是偶然之中还有偶然？那么，究竟是由于信息量太大而暂时无法计算我们的命运，还是因为事物就像那个无限数列一样无法计算？我期待着有人能够告诉我我的宿命。

今天突然想起来要把以前的一些怪想法记录下来。正好刚刚才做完一道题，现在有空就来回忆一下。

就从所谓“观测者的存在影响物体的运动”开始，这就是说，如果一个观测者处在某个体系之中，那么这个体系中的物体会受到这个观测者的影响。从而有“测不准”的说法，也就是不能同时准确地度量某些相关的量。表面上看并没有什么，因为从万有引力理论中我们知道所谓“引力场”的概念，也就是一个物体无论周围有没有其它的物体，总是会形成一种物质场来改变周围的环境。从这个想法进行类比，观测者影响环境是理所当然的。同时环境也会影响观测者，这一点似乎是肯定的，因为观测者和体系之间并没有明确的界限。

但是我们自身是否仍然受到自身的影响呢？或者说我们自身就是受到了自身的束缚呢？这并不仅仅是人的问题，人只是一个观测者，但是物体的存在是不是也有类似的规律？许多数学理论中都有“封闭性”这一个说法，元素与元素之间的运算和关系，总还是在既有的体系之中。推至理论的角度来看，人通过自身观测宇宙而得到的一系列规律，是否也具有封闭性？就好比弈棋之道，在于超然于棋盘之外，如果只是守在棋盘之上，总是要被束缚的。如果说这些理论规律都是封闭的，那么怎样才能破开这些关系，寻找到更进一步的规律？

这里可能有点乱，我稍微总结一下，就是由于物体一定是处在某个体系之中，并且两者之间是共成一体又相互作用的，而如果这个体系中的一切具有封闭性的话，那么物体永远也没有办法突破到外界，所以会有无限的概念。这里的无限听上去有点诡辩的色彩，就像是芝诺的命题：阿基里斯追赶乌龟，明明就在前方，但是由于受到规则的限制，始终不能迈出关键的一步。

我们现有的科学理论体系，就好像是我们观测世界所画出来的一幅画，世界是怎么样，就只能画成什么样，而且还要受到画画的人的限制，不可能一模一样，总会因为手法的缘故有些形似而神不似。我们就这样画出了一个科学的大厦，这只是存在于我们脑海中的理想世界。但是世界终归是要从世界之外才能了解它，类似于人永远也不可能明白人在想什么，因为人就是人，不是造物主。

但是我们暂时还只能在这个世界中的世界中寻找出口，前往未知的路。