Feb 24

戴德金分割理论（Dedekind Cut）

Art of Science 1 Comments

对于实数集这个概念，我们有一些很好的基本性质：

  • 实数集是一个有序集；
  • 实数集是稠密的；
  • 实数集中四则运算具有封闭性。

当然，这些性质并不能严格地给出实数的定义，戴德金分割理论正是为此而产生的一个理论。

戴德金理论是一种对集合进行划分的方法。前提是这个集合是可以严格排序的。方法把待分割的集合分成两个交集为空且自身不为空的集合A和B，而且A中的任何元素都比B中的元素小。我们令全集为U，那么形式化的：

  • $A\cup B=U$；
  • $A\cap B=\phi$，$A,B\neq \phi$；
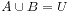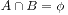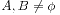  • 对于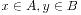$x\in A,y\in B$，必然有x<y。

显然，对于A和B中最大值和最小值的情况有四种情况。

首先，整数集、有理数集、实数集都是存在戴德金分割的。对于整数集来说，由于不存在稠密性，分割中A必定存在最大值，B必定存在最小值。我们可以把相应的最值称为边界数。而对于有理数集和实数集而言，要么A中存在最大值，要么B中存在最小值，必定满足且仅满足其中的一个。这很容易证明，如果同时满足，那么根据有理数集和实数集的稠密性，两个边界数中必定还存在一个既不属于A又不属于B的数，与分割的定义矛盾。

所以我们可以根据有理数集的戴德金分割来定义实数集。

对于有理数集Q的一个戴德金分割，如果A中存在最大值或者B中存在最小值，那么就定义了一个有理数；如果A中没有最大值，B中也没有最小值，那么就定义了一个无理数。实际上，分割的情况不外乎下面三种：

  • $A=\{x<r\},B=\{x\geq r\}$；
  • $A=\{x\leq r\},B=\{x>r\}$；
  • $A=\{x<r\},B=\{x>r\}$。

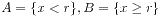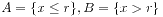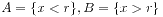前面两种情况就定义了有理数r，最后一种情况则定义了无理数r。之所以会有这种区别，是因为实数集具有连续性。

如果我们规定有理数集的戴德金分割不允许集合A有边界数，那么可以建立分割和实数的一一对应关系，在有理数的基础上定义了实数，这为数学分析奠定了基础。

Feb 22

最小树形图

Art of Science 1 Comments

最小树形图就是最小生成树在带权有向图上面的变种，也就是在有向图上找出一个边权和最小的有向树。这个问题需要给定一个带权的有向图以及有向树的根节点v。所谓有向树是指除了叶节点以外，所有节点都有指向其孩子节点的有向边。专业一点的说，“有向树（Directed Tree）是一个用于定义数据流或流程的逻辑结构。数据流的源点是根。数据流是单向分支离开根部到达目标，这个目标就是有向树的叶子。”。

求解最小树形图的第一个算法是1965年朱永津和刘振宏提出的复杂度为O(VE)的算法，该算法被称为朱-刘算法。在实现过程中，我们也可以表达为O(V3)的复杂度。

首先我们需要判断解是否存在。为了解决这个问题，我们只需要从指定的根节点v除法遍历一次就可以了。如果所有节点都可以被访问，那么解显然存在，否则不存在。另外，图中所有的自环也必须清除，因为这些自环显然不可能是最小树形图中的边。如果不知道什么是自环，请自行查阅图论相关定义。消除自环的目的是保证算法的时间复杂度。

下面是算法的流程：

  1. 对于图中除了根节点v以外的节点，选择一条权值最小的入边。所有被选择的边构成了一个子图，如果这个子图不含有有向环，那么这就是问题的解，算法结束；否则进行下一步。
  2. 我们需要收缩有向环，并且用一个新节点来代替。对于环中的点x，假定其选择边的权值为w0，y为环外的点，z为环收缩后新的节点。如果存在边<x,y>，那么<z,y>的边权值与<x,y>相同。如果存在边<y,x>且权值为w，那么新边<y,z>的权值就是w-w0。
  3. 重复执行1、2两个步骤。

要保证算法O(VE)的复杂度，要做到找最小入边O(E)，找环O(V)，收缩O(E)。再加上由于收缩环最多只进行V-1次（自环已经被消除），所以时间复杂度为O(VE)。在步骤2中，x的出边权值不变是因为收缩环并没有影响边所指向的节点，而入边的权值之所以要变小，是因为当新边被选择之后，x原来选择的入边就会被取消选择，所以实际花费的代价就是w-w0。

以下是2道可以提交的题目。

  • [UVa]11183 - Teen Girl Squad
  • [PKU]3164 - Command Network
Feb 16

《初等数论》读书笔记：同余

Art of Science 1 Comments

这里的同余包含了同余和同余方程两个章节。

基本的同余概念可以从带余除法中推导出来。使用带余除法，我们可以得到同余式的相关运算性质。

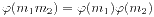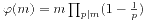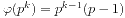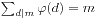接下来，我们引入同余类和剩余系的概念。剩余系主要是介绍了既约剩余系。我们从既约剩余系的定义中引出了Euler函数。Euler函数是一个积性函数，也就是说如果(m1,m2)=1，那么$\varphi(m_1m_2)=\varphi(m_1)\varphi(m_2)$。Euler函数有如下的计算式 $\varphi(m)=m\prod_{p|m}(1-\frac{1}{p})$，特别的，当m=pk时，我们有$\varphi(p^k)=p^{k-1}(p-1)$。我们还有\sum_{d|m}\varphi(d)=m，我们可以从中看出Mobius函数的一点影子。

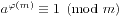接下来，我们由一个性质得到了一个重要的定理：Fermat-Euler定理。这个性质是，对于一个模m，它的任何一个既约剩余系中所有元素的乘积模m是相同的，也可以表述为(a,m)=1时，x遍历m的既约剩余系当且仅当ax遍历m的既约剩余系。我们得到$a^{\varphi(m)}\equiv 1\pmod{m}$，以及当m=p时，对于任意的a，我们有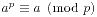$a^p\equiv a\pmod{p}$。前面的式子被称为Fermat小定理，后面的式子被称为Euler定理。

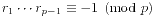Wilson定理是如下的内容$r_1\cdots r_{p-1}\equiv -1\pmod{p}$，也就是对于一个素数p>3，它的既约剩余系中所有数的乘积模p为-1。特别的，我们有$(p-1)!\equiv -1\pmod{p}$。事实上，p不取1,2,4,pk,2pk时，p的既约剩余系的积模p得1。Wilson虽然不能用来高效地检验素数，但是可以被用来简化运算。

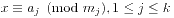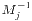同余方程是多项式同余的形式。其最简单的形式是一次同余方程。我们可以用带余除法和辗转相除法得到其解。中国剩余定理用来求解一次同余方程组。对于一个一次同余方程组$x\equiv a_j\pmod{m_j},1\leq j\leq k$，这里m1,...,mk两两既约。那么其解为$x\equiv M_1M_1^{-1}a_1+\cdots+M_kM_k^{-1}a_k\pmod{m}$，m=m1...mk，m=mjMj，以及$M_j^{-1}$是Mj模mj的逆。这个解的正确性容易带入验证。如果m1,...,mk并非两两既约，则可以化为各个方程都是模pk的形式更加方便。

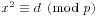关于模为素数的二次同余方程，我们只需要讨论$x^2\equiv d\pmod{p}$的形式。对于模p，如果一个d能使得方程有解，那么我们称d为模p的二次剩余；否则d就是模p的二次非剩余。我们可以用Euler判别法来进行判断。如果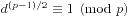$d^{(p-1)/2}\equiv 1\pmod{p}$，那么d就是模p的二次剩余；如果$d^{(p-1)/2}\equiv -1\pmod{p}$，那么d就是模p的二次非剩余。

我们还可以引进Legendre符号和Jacobi符号来进行进一步的研究。Gauss二次互反律也是进一步的探讨对象。具体内容可以参见原书或者nmbr.rar。

Feb 13

《初等数论》读书笔记：整除

Art of Science 0 Comments

一上来作者介绍了Peano公理。这个公理告诉我们，自然数就是一个有起点的、存在后继的无限整数集合。自然数的性质都可以通过这个抽象的定义来推导。我们一般使用1,2,3,...，是因为它本身具有代表性。至于0的问题，一般在不涉及的情况下不考虑。从Peano公理我们得到了数学归纳法和两个自然数的原理：最小和最大自然数原理。数学归纳法在数论当中可以用来证明多项的命题，也可以用来证明取值范围是固定连续整数域的恒等式或者命题。

接下来是整除的概念，我们一般是把它和带余除法结合起来看。从基本定义我们就可以推导很多有用的性质。从整除我们得到一类非常有用的数：素数。素数具有很多的性质。关于素数的判定也是一个很重要的课题，一般而言我们有试除法、Fermat素性检验、Miller-Rabin素性检验。A.K.S算法是第一个被证明的可以在多项式时间内检验素数的算法。

接下来作者介绍了公约数和公倍数的理论。我们又得到了互素的概念。这在书中仅仅是一个先头的简单介绍，作者接着引进了带余除法的概念。这是一个非常有用的概念，我们可以通过它进行很多讨论余数的证明。整数分类也是来自于带余除法。有了带余除法的概念之后，我们就可以讨论很多情况下余数的性质。带余除法是初等数论中极其重要的内容。

接下来就是辗转相除法。这也是一个来自于带余除法的内容。

我们现在可以建立最大公约数理论。带余除法、辗转相除法和整系数线性组合是3种很容易被引进的方法。我们需要了解的是，一个集合中数的最大公约数就是这些数的整系数线性组合中最小的那一个，也就是$(a_1,\cdots,a_k)=\min\{s=a_1x_1+\cdots+a_kx_k:x_j\in Z(1\leq j\leq k),s>0\}$。

现在进入到了算术基本定理，我们现在可以用素数的性质来对整数进行分析。由于算术基本定理的存在，我们一定可以通过分析素数的性质来得到相关整数的性质。这里需要介绍一下除数和函数$\sigma(n)=\prod_{j=1}^{r}\frac{p_j^{a_j+1}-1}{p_j-1}$。

对于本章最后的[x]函数的分析，就不再过多的叙述，因为都是很普通的内容。而对于n!的分解式，要能够体会其中蕴含的缩小规模的递归思想。

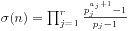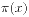最后是容斥原理和$\pi(x)$的分析。容斥原理更多的是使用在组合数学当中。而$\pi(x)$的计算需要相应的推导，具体内容可以参见书中。或者可以参见我的另外一个笔记：nmbr.rar。

Feb 11

泰州冬令营归来

Spirit and Thinking 0 Comments

我这几天一直在泰州参加冬令营，所以也没有什么时间来整理一些东西。接下来会放出一些冬令营的东西。

我们住在宾馆，有网线但是非常不稳定，经常掉线。我们只好在学校里面用无线。

冬令营和以往一样，还是没有什么太大的变化，题目也都是比较经典的老题。现在江苏的冬令营是越来越大规模了，所以学生的素质也下降了不少。

这里是我这次讲的数论的内容：nmbr.rar，大家有兴趣可以看看。