阶乘的最后一位非零位就是n!的数值中从右到左第一个非零的数字。比如,7!=5040,那么7!的最后一位非零位就是4。一个粗略的想法是每10个数字的末尾数相乘是一个定植,那么n个连续的自然数也可以类似地转化,接着就可以求出。这个想法无疑是错误的,因为注意到2*5=10,而12*15=180,两个结果的末位非零数并不相等,所以末尾数相乘不是10个数字为一个循环。
如果要求n!末尾0的个数,就是一个非常简单的问题。因为10=2*5,我们只要求出2和5在n!的标准分解式中出现了多少次,就可以求出末尾0的个数。而又由于2出现的次数一定比5多,所以,只需要求出5出现的次数。例如,n=2005,那么5出现的次数就是401+80+16+3=500个,也就是2005!的末尾有500个0。
现在我们对n!的情况有了一个大概的认识。简单点来说,n!=2a5bc,这里c是所有不包含2和5的因数的乘积。显然,最后一位非零位取决于2a-bc的最后一位。我们只要想办法求出c,n!的非零位就很容易了。注意到如果一个数字的末位如果是3,5,7,9,那么一定是c的组成部分。但是这些数字还不够,因为当2和5被提取之后,又产生了新的末位为3,5,7,9的数字,所以我们要逐次的提取2和5这两个因数,然后算出每种情况下末位为3,5,7,9的数字的数量。
回忆求2这个因数的办法,就是逐次的除以2来缩小规模。例如,当n=2005时,只含有一个因数2的数一共有1002个,含有两个因数2的数字一共有501个,……。也就是一种递归的思想,不过这里是尾递归,可以消除。下面关于如何求出末位为3,5,7,9的数字的方法就不再赘述了,直接给出代码,相信还是能够理解的。
//co2,co3,co5,co7,co9分别表示了2,3,5,7,9的个数。
static int co2,co3,co5,co7,co9;
void calc(int n) {
if (n<=1) return;
for (int i = n; i>0; i /= 5) {
int p = i/10,q = i%10;
co3 = p+(int)(q>=3);
co5 = p+(int)(q>=5);
co7 = p+(int)(q>=7);
co9 = p+(int)(q>=9);
}
co2 += n/2;
calc(n/2);
}
至此,问题转化为了2,3,5,7,9之间幂的关系,注意到32n=9n,而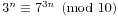 ,所以又可以转化为3的幂,下面的过程就简单多了。
,所以又可以转化为3的幂,下面的过程就简单多了。
其实求n!的最后一位非零位还有其它的方法,但其实也不外乎利用递归的思想提取因数,来达到化大为小的目的。有兴趣的可以去Google一下,可以找到很多资料。

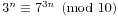 ,所以又可以转化为3的幂,下面的过程就简单多了。
,所以又可以转化为3的幂,下面的过程就简单多了。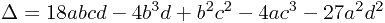
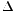 的正负情况:
的正负情况: ,那么只有一个实数解,另外两个解是复数解。
,那么只有一个实数解,另外两个解是复数解。 ,存在重根,但是所有解都是实数。
,存在重根,但是所有解都是实数。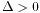 ,存在三个实数解。
,存在三个实数解。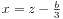 ,就可以消去二次项,从而得到z3+pz+q=0。我们令z=u+v,得到(u+v)3+p(u+v)+q=0,因式分解得到(u3+v3+q)+(u+v)(3uv+p)=0,由于u,v的值是不确定的,所以我们可以再加上一个条件3uv+p=0,这样我们得到u3+v3+q=0。至此,我们可以解出u和v,可以接下来得到三次方程的解。需要注意的是,在复数域中,求解u,v的时候要考虑三种情况。
,就可以消去二次项,从而得到z3+pz+q=0。我们令z=u+v,得到(u+v)3+p(u+v)+q=0,因式分解得到(u3+v3+q)+(u+v)(3uv+p)=0,由于u,v的值是不确定的,所以我们可以再加上一个条件3uv+p=0,这样我们得到u3+v3+q=0。至此,我们可以解出u和v,可以接下来得到三次方程的解。需要注意的是,在复数域中,求解u,v的时候要考虑三种情况。![$x=\sqrt[3]{A}+\sqrt[3]{B}$ $x=\sqrt[3]{A}+\sqrt[3]{B}$](/user_files/rchardx/epics/9b0aea1c549332fea9d2eabf9d9fc2bc0a0b3225.png) 。那么我们得到
。那么我们得到![$x^3=(A+B)+3\sqrt[3]{AB}x$ $x^3=(A+B)+3\sqrt[3]{AB}x$](/user_files/rchardx/epics/9a99fd141a4ade454372640ec7d512aa9fc3f1d3.png) 。移项化简得到x3+px+q=0的形式,这里
。移项化简得到x3+px+q=0的形式,这里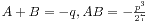 。所以可以化归为二次方程两个根的韦达定理。从而进一步就可以求出用p,q表示的x的解。这里A,B只是起到了一个中间变量的作用。
。所以可以化归为二次方程两个根的韦达定理。从而进一步就可以求出用p,q表示的x的解。这里A,B只是起到了一个中间变量的作用。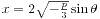 形式的解,其中
形式的解,其中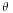 满足
满足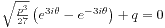 。但其实这也只是将变量x用
。但其实这也只是将变量x用